Two infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
μ0i2π√2
μ0i4π√2
μ0i2√2π
μ0i2π
The correct Answer is:D
To solve the problem, we need to find the magnetic induction (magnetic field) at a point that is equidistant from two infinitely long parallel wires carrying equal currents in the same direction. Here’s a step-by-step solution:
Step 1: Understand the setup
We have two parallel wires separated by a distance of 2 m, and we are interested in the magnetic field at a point that is at a distance of √2m from each wire.
Step 2: Magnetic field due to a single wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Calculate the magnetic field from each wire
Since the point is at a distance of √2m from each wire, we can substitute r=√2 into the formula:
B1=μ0I2π√2
for wire 1 and
B2=μ0I2π√2
for wire 2.
Step 4: Determine the direction of the magnetic fields
Since both wires carry current in the same direction, the magnetic fields at the point of interest will be in opposite directions. We can use the right-hand rule to determine the direction of the magnetic fields.
Step 5: Calculate the net magnetic field
The net magnetic field Bnet at the point is the vector sum of B1 and B2. Since they are in opposite directions, we can write:
Bnet=B1−B2=μ0I2π√2−μ0I2π√2=0
However, this is incorrect because we need to consider the components of the magnetic fields.
Step 6: Resolve the components
The angle θ between the line connecting the wires and the line to the point is 45∘ (since the point is at equal distances from both wires). The effective magnetic field from each wire at the point can be resolved into components. The vertical components will cancel out, and the horizontal components will add up.
The effective magnetic field from each wire along the line connecting the two wires is:
Beffective=Bcos(45∘)=μ0I2π√2⋅1√2=μ0I4π
Step 7: Calculate the total magnetic field
Since there are two wires contributing equally to the magnetic field in the same direction:
Bnet=2⋅Beffective=2⋅μ0I4π=μ0I2π
Final Answer
Thus, the magnitude of the magnetic induction at the point is:
Bnet=μ0I2π
Conclusion
The correct option is Option 4: μ0I2π.
---
We have two parallel wires separated by a distance of 2 m, and we are interested in the magnetic field at a point that is at a distance of √2m from each wire.
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Since the point is at a distance of √2m from each wire, we can substitute r=√2 into the formula:
B1=μ0I2π√2
for wire 1 and
B2=μ0I2π√2
for wire 2.
Since both wires carry current in the same direction, the magnetic fields at the point of interest will be in opposite directions. We can use the right-hand rule to determine the direction of the magnetic fields.
The net magnetic field Bnet at the point is the vector sum of B1 and B2. Since they are in opposite directions, we can write:
Bnet=B1−B2=μ0I2π√2−μ0I2π√2=0
However, this is incorrect because we need to consider the components of the magnetic fields.
The angle θ between the line connecting the wires and the line to the point is 45∘ (since the point is at equal distances from both wires). The effective magnetic field from each wire at the point can be resolved into components. The vertical components will cancel out, and the horizontal components will add up.
Beffective=Bcos(45∘)=μ0I2π√2⋅1√2=μ0I4π
Since there are two wires contributing equally to the magnetic field in the same direction:
Bnet=2⋅Beffective=2⋅μ0I4π=μ0I2π
Thus, the magnitude of the magnetic induction at the point is:
Bnet=μ0I2π
The correct option is Option 4: μ0I2π.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Two long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
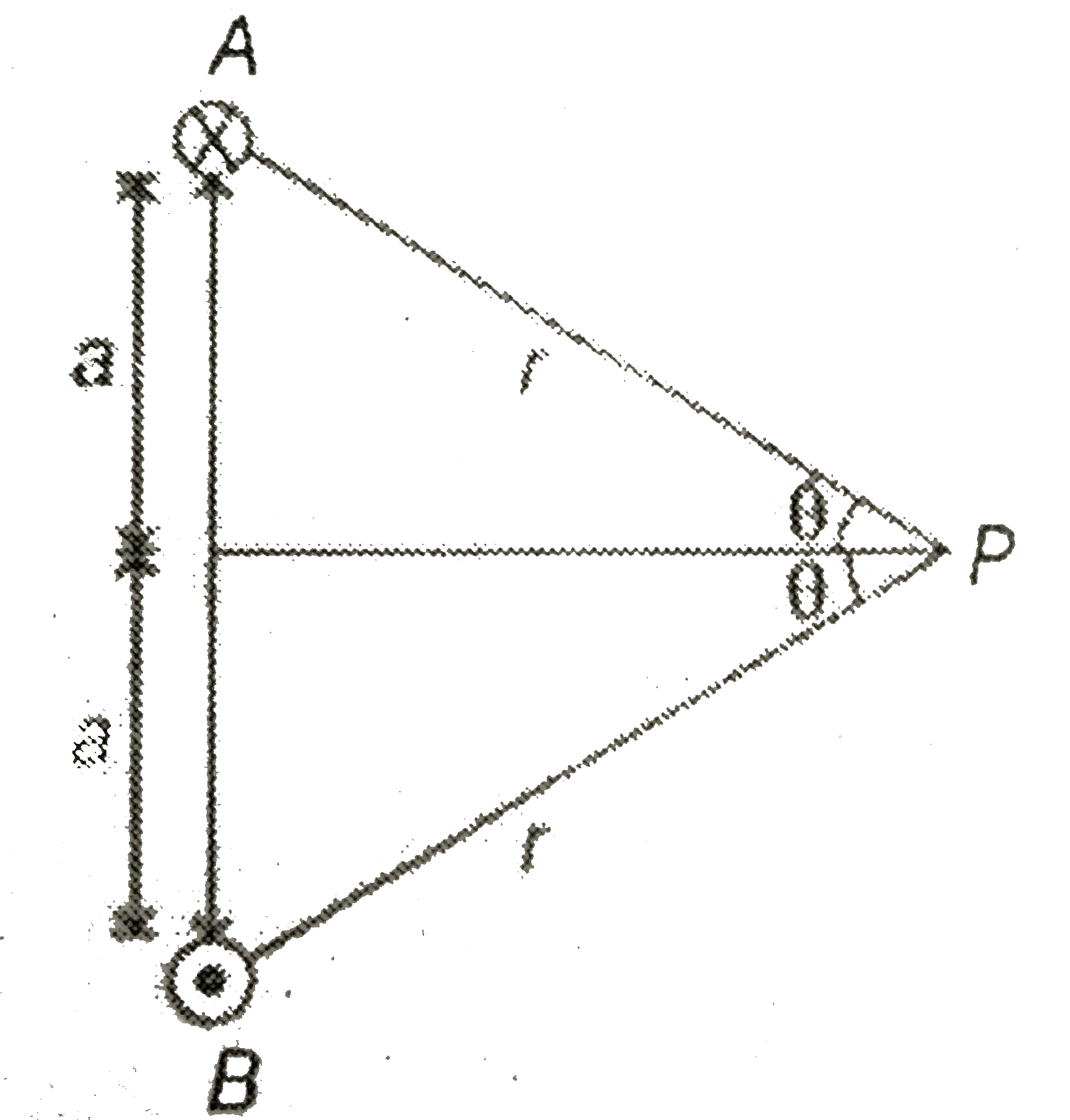 View Solution
View SolutionTwo long wires are placed parallel to each other with a distance 1 m between them. The wires carry equal current 1 A in the same direction. The magnetic field intensity at a point P which is equidistant from the wires is 1.6×10−7T. Then, the distance of this point from any one of the wires is _________ m.
[Permeability of vacuum, μ0=4π×10−7T−m/A]View SolutionTwo long parallel conductors carry currents I and 2I in the same direction. The magnetic induction at a point exactly mid way between them is B. If the current in the first conductor is reversed in direction, the magnetic induction at the same point will be
View SolutionTwo infinetely long, parallel wires are lying on the ground at distance a=1cm apart as shown in Fig. A third wire, of length L=10m and mass 400g, carries a current of I1=100A and is levitated above the first two wires, at a horizontal position midway between them. The infinitely long wires carry equal currents I1 in the same directions, but in the direction opposite that in the leviated wire. What current must the infinately long wires carry so that the three wires form an equilateral triangle?
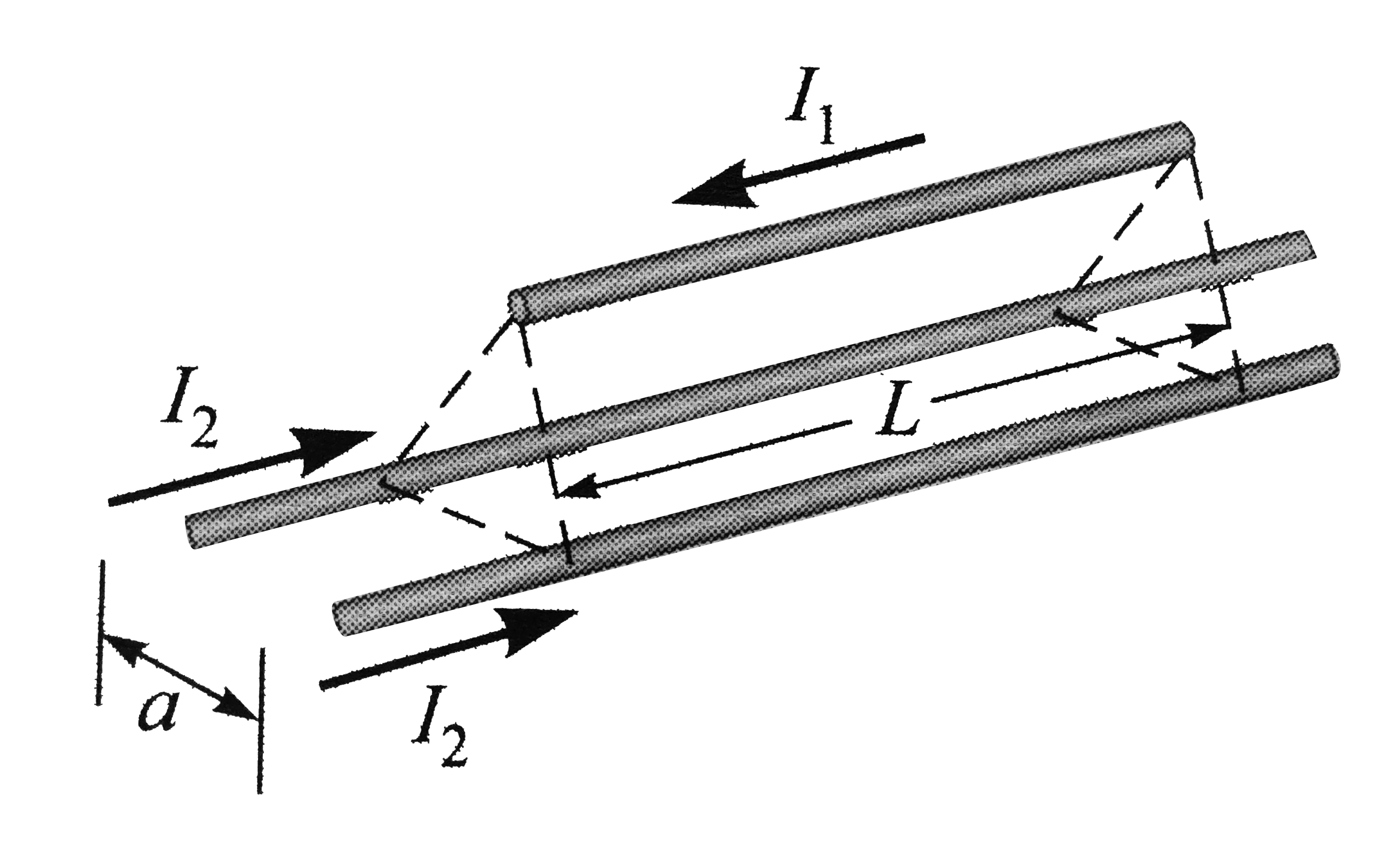
 View Solution
View Solution

