Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
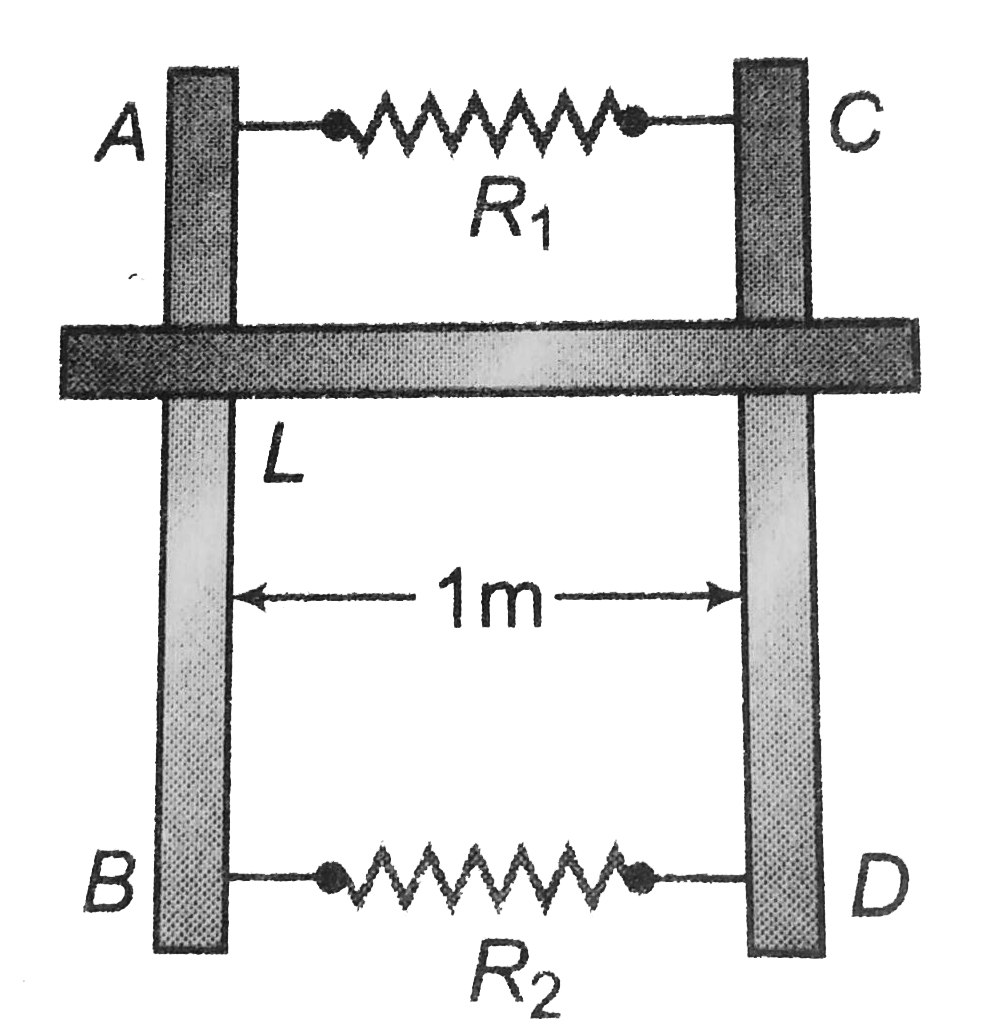
The value of R1 is
When rod moves downward under gravity then motional emf is generated across its ends and current starts flowing through the rod. Magnetic force thus acting on the rod tries to oppose its motion. As speed of rod increases, emf induced also increases which in turn increases the current flowing through the rod which further increases magnetic force acting on the rod. At a particular speed magnetic force becomes equal to the weight of the rod and then rod attains terminal velocity.
Hence for terminal velocity we can write the following equation:
IlB = mg
⇒I=mglB=0.2×9.81×0.6=1.960.6amp
If e is the emf induced in the rod then el will be the power delivered by the rod as a source of emf and this will be equal to the sum of the power dissipated across both the resistors. Hence we can write the following:
eI=P1+P2
⇒e×1.960.6=1.2+0.76
⇒e×1.960.6=1.96
⇒ e = 0.6 V
Motional emf induced across the length of rod can also be written as Bvl, where v is the velocity of rod perpendicular to its length. Hence terminal velocity can be calculated as follows:
Bvl = 0.6
⇒v=0.60.6×1=1m/s
Hence rod attains a terminal velocity of 1m/s.
Rate of heat dissipation across a resistor when e potential difference is applied across its ends can be written as follows:
P=e2R⇒R=e2P
Hence both the resistances can be calculated as follows:
R1=e2P1=(0.6)21.2=0.3Ω
and R2=e2P2=(0.6)20.76=0.47
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Very Short Answer Questions Carrying I mark)44videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Additional Questions (Carrying I mark))11videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)5videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
Similar Questions
Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at two ends by resistanace (R1)and(R2) as shown in fig. A horizontal metallic bar L of mass 0.2 kg slides without froction vertically down the rails under the action of gravity. THere is a uniform horizontal magnetic field of 0.6 Tesla perpendicular to the plane of the rails. It is observed taht when the teminal velocity is attained, the power dissipated in (R1)and(R2) are 0.6 watt and 1.2 watt respectively. Find the terminal velocity of the bar L and the values of (R1)and(R2).
 View Solution
View SolutionTwo parallel vertical metellic rails AB and CD are separated by 1m. They are connecting at two ends by resistances R1 and R2 as shown in Fig. 3.96. A horizontal metallic bar L mas 0.2kg slides without friction vertically down the rails under the action of gravity. There is a uniform horozontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, thwe power dissipated in R1andR2 are 0.76and1.2W, respectively. Find the terminal velocity of the bar L and the values of R1andR2.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
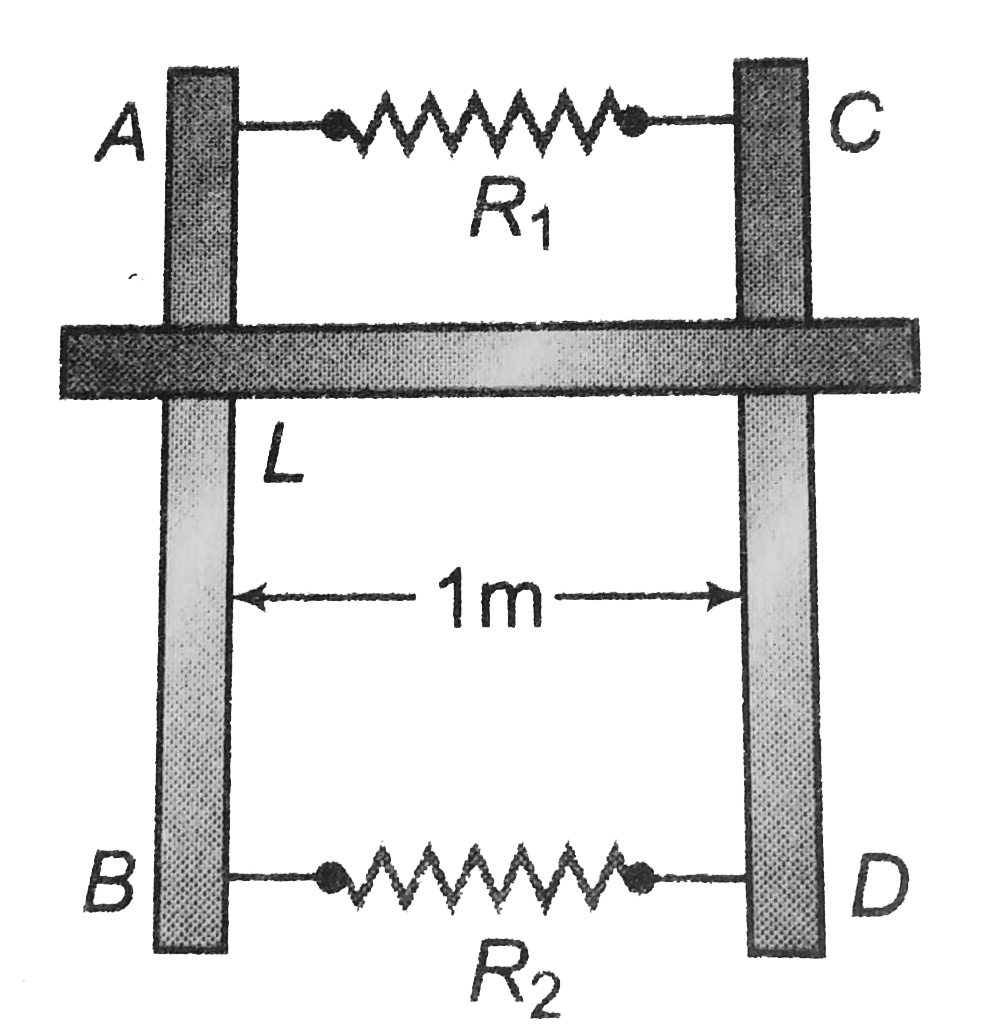
The terminal velocity fo the bar L will beA2m/sB3m/sC1m/sDNone of these - Question 2 - Select One
A conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of
 AmgRBlBmgRBl2CmgRB2l2DmgRB2l
AmgRBlBmgRBl2CmgRB2l2DmgRB2l - Question 3 - Select One
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRcosθB2l2BmgRsinθB2l2CmgRtanθB2l2DmgRcotθB2l2
Two parallel vertivcal inetallic ralis AB and CD are serparated by l= 1 m . They are connected at the ends by resistance R1 and R2 as show in the figure . A horizationl metallic bar L of mass m= 0.2 kg slides without friction vertically down the rails under the action of gravity . These is a unifrom horizonal magnetic field of a B=0.6T perpendicular to the plane to rails . It is observed that when the termainal veloctity is attained , the power disspated in R1 and R2 are P1=0.76W and P2=1.2W respectively . Find the terminal velocity of bar L and the values of R1 and R2
View SolutionA copper bar of mass m sides under gravity on two smooth parallel rails l distance apart and set at angle α to the horizontal . At the lop , the rails are joined by a resistor R. Calculate the steady velocity of the bar the n when there is a unifrom magnetic field B perpedicular to the plane of the rails .
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isView SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
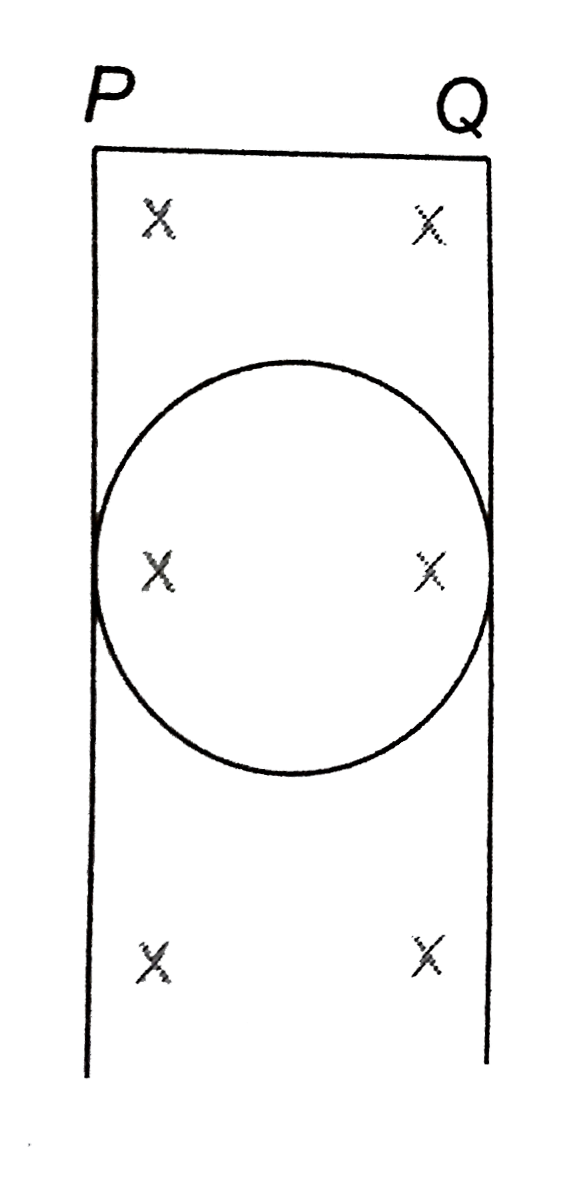 View Solution
View SolutionTwo vertical conducting rails separted by distance 1.0m are placed parallel to z-axis as shown in figure. At z=0, a capacitor of 0.15F is connected between the rails and a metal rod of mass 100g placed across the rails slides down along the rails. if a constant magnetic fields of 2.0 T exists perpendicular to the plane of the rails, what is the acceleration of the rod?
 View Solution
View Solution

