Two skaters, one with mass 75 kg and the other with mass 40 kg, stand on an ice rink holding a pole of length 10 m and negligible mass. Starting from the ends of the pole. the skaters pull themselves along the pole until they meet. How far does the 40 kg skater move?
The correct Answer is:6.5 m
To solve the problem of how far the 40 kg skater moves when both skaters pull themselves along the pole until they meet, we can follow these steps:
Step 1: Understand the System
We have two skaters with masses:
- Skater 1 (M1) = 75 kg
- Skater 2 (M2) = 40 kg
They are initially at the ends of a 10 m pole. We need to find out how far the 40 kg skater (M2) moves towards the 75 kg skater (M1).
Step 2: Set Up the Coordinate System
Let’s set up a coordinate system along the pole:
- Position of M1 (75 kg) at x = 0 m (left end)
- Position of M2 (40 kg) at x = 10 m (right end)
Step 3: Define the Displacements
Let:
- The distance moved by M2 (40 kg) towards M1 be x.
- The distance moved by M1 (75 kg) towards M2 will then be (10 - x) since the total length of the pole is 10 m.
Step 4: Apply the Center of Mass Concept
Since there are no external forces acting on the system (the skaters are pulling themselves), the center of mass of the system will remain stationary. The formula for the center of mass (CM) of a two-particle system is given by:
xCM=m1x1+m2x2m1+m2
Step 5: Calculate the Initial Position of the Center of Mass
Initially, the center of mass (CM) is calculated as follows:
xCM=(75kg⋅0)+(40kg⋅10m)75kg+40kg=0+400115=400115≈3.48m
Step 6: Set Up the Equation for Final Position of the Center of Mass
After they meet, the new positions will be:
- M1 will have moved (10 - x) m to the right.
- M2 will have moved x m to the left.
The new position of the center of mass will still be:
xCM=(75⋅(10−x))+(40⋅x)115
Step 7: Set the Two Center of Mass Equations Equal
Since the center of mass does not change position:
(75⋅(10−x))+(40⋅x)115=400115
Step 8: Solve for x
Multiply both sides by 115 to eliminate the denominator:
75(10−x)+40x=400
Expanding and simplifying:
750−75x+40x=400
750−35x=400
−35x=400−750
−35x=−350
x=35035=10
Step 9: Calculate the Distance M2 Moves
Thus, the distance moved by the 40 kg skater (M2) is:
x=10m
Final Answer
The 40 kg skater moves 6.5 m towards the 75 kg skater.
---
We have two skaters with masses:
- Skater 1 (M1) = 75 kg
- Skater 2 (M2) = 40 kg
Let’s set up a coordinate system along the pole:
- Position of M1 (75 kg) at x = 0 m (left end)
- Position of M2 (40 kg) at x = 10 m (right end)
Let:
- The distance moved by M2 (40 kg) towards M1 be x.
- The distance moved by M1 (75 kg) towards M2 will then be (10 - x) since the total length of the pole is 10 m.
Since there are no external forces acting on the system (the skaters are pulling themselves), the center of mass of the system will remain stationary. The formula for the center of mass (CM) of a two-particle system is given by:
Initially, the center of mass (CM) is calculated as follows:
After they meet, the new positions will be:
- M1 will have moved (10 - x) m to the right.
- M2 will have moved x m to the left.
Since the center of mass does not change position:
Multiply both sides by 115 to eliminate the denominator:
750−35x=400
−35x=400−750
−35x=−350
x=35035=10
Thus, the distance moved by the 40 kg skater (M2) is:
The 40 kg skater moves 6.5 m towards the 75 kg skater.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
Two particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
View SolutionA man with mass 85 kg stands on a platform with mass 25 kg. He pulls on the free end of a rope that runs over a pulley on the ceiling and has its other end fastened to the platform. The mass of the rope and the mass of the pulley can be neglected, and the pulley is frictionless. With what force does he have to pull so that he and the platform have an upward acceleration of 2.2ms2. (Take g=10ms2)
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of mass 5 kg and 10 kg respectively are attached to the twoends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
A50 cmB67 cmC80 cmD33 cm - Question 2 - Select One
A boy of mass 50kg is standing at one end of a boat of length 9m and mass 400kg. He runs to the other end. The distance through which the centre of mass of the boat boy system moves is
A0B1mC2mD3m - Question 3 - Select One
A string of length 10.0 m and mass 1.25kg stretched with a tension of 50N. If a transverse pulse is created at one end of the string, how long does it take to reach the other end ?
A0.5sB1.0sC1.5sD2.0s
A man of mass 85kg stands on one end of a uniform board of length 2m and mass 15kg. The other end is tied to the floor by a steel cable, and the board is supported from below just 0.5 m from the cable end (see figure).
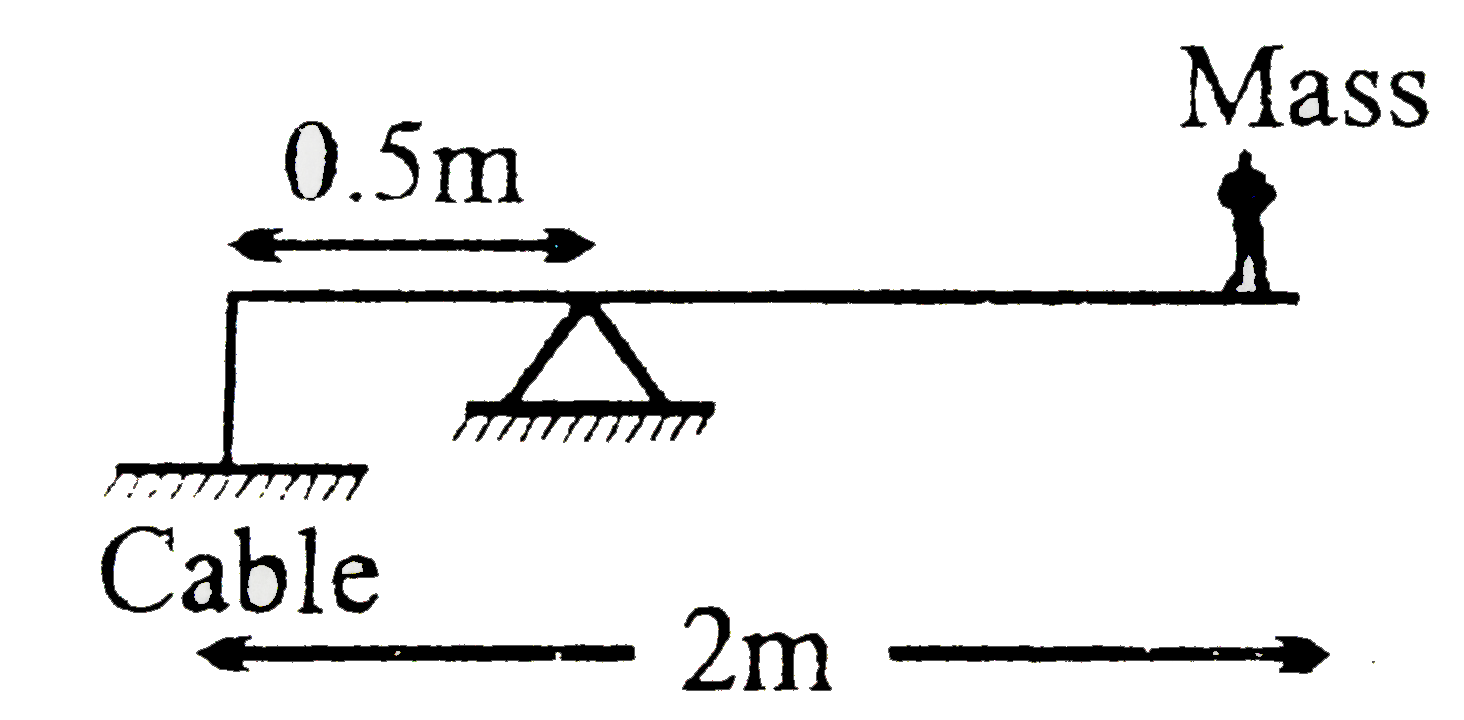 View Solution
View SolutionTwo skaters on frictionless ice hold opposite ends of a pole of negligible mass. An axis runs along it, with the origin at the center of mass of the two-skater system. One skater, Fred , weighs twice as much as the other skater, Ethel. Where do the skaters meet if (a) Fred pulls hand over along the pole so as to draw himself to Ethel , (b) Ethel pulls hand over hand to draw herself to Fred, and (c ) both skaters pull hand over hand ?
View SolutionIn Fig. 10-78, two skaters, each of mass 50 kg, approach each other along parallel paths separated by 3.0 m. They have opposite velocities of 1.4 m/s each. One skater carries one end of a long pole of negligible mass, and the other skater grabs the other end as she passes. The skaters then rotate around the center of the pole. Assume that the friction between skates and ice is negligible. What are (a)the radius of the circle, (b) the angular speed of the skaters, and ( c) the kinetic energy of the two skater system? Next, the skaters pull along the pole unyil they are separated by 1.0 m. What then are (d) their angular speed and (e) the kinetic energy of the system? (f) What provided the energy for the increased kinetic energy?
 View Solution
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionA man of 50 kg is standing at one end on a boat of length 25m and mass 200 kg. If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat. The final velocity of the boat is
View Solution

