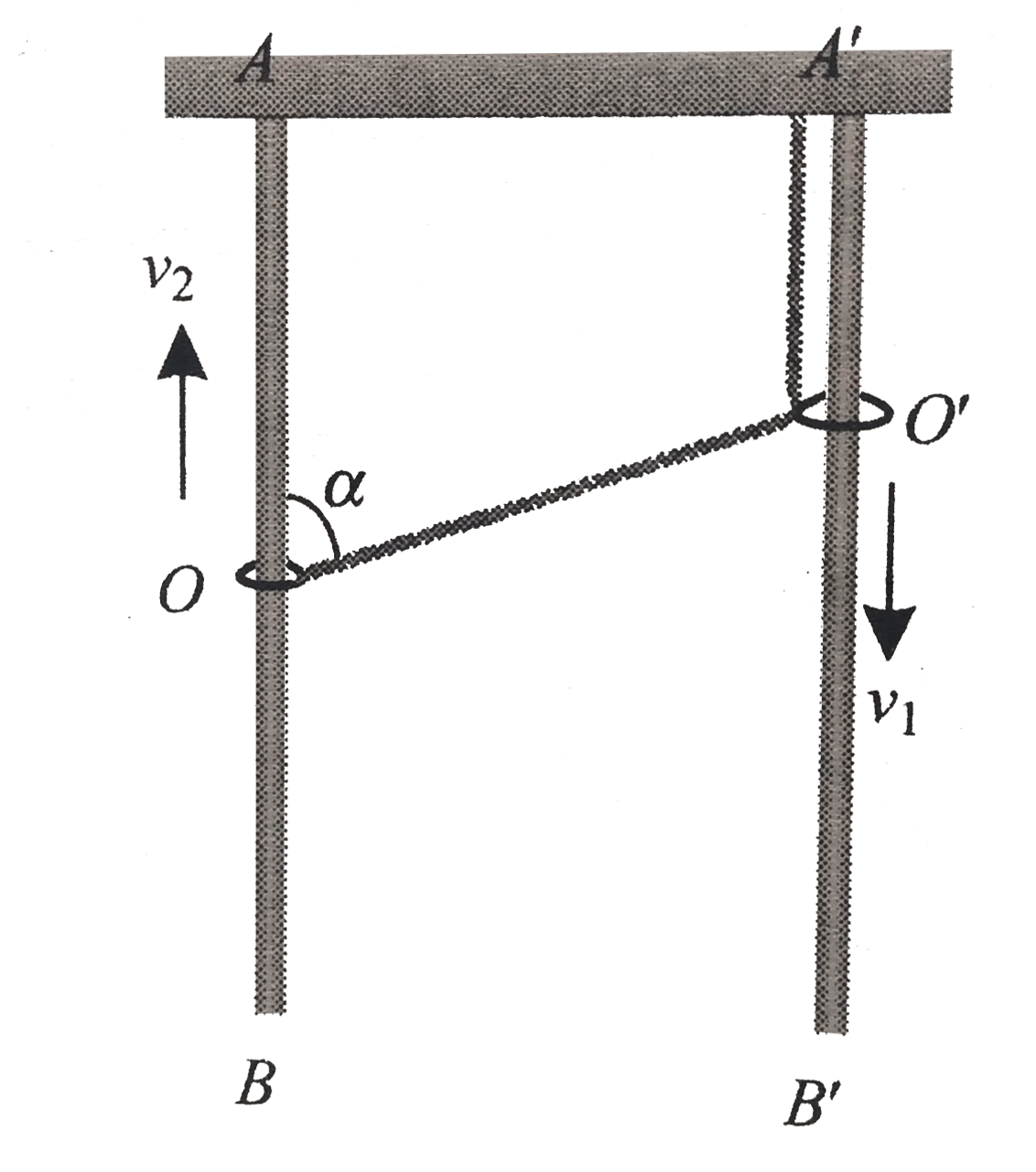
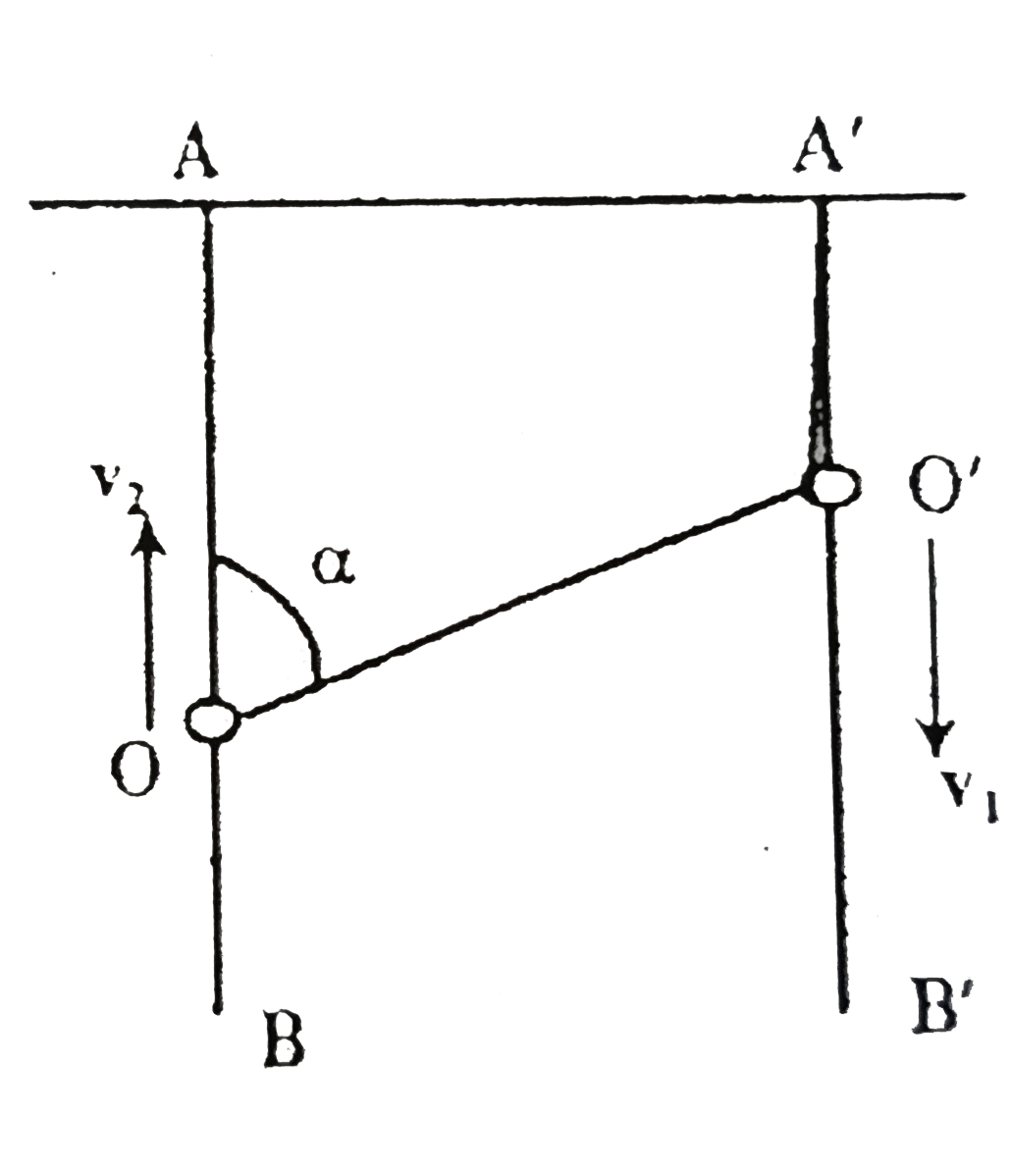
Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v1, then velocity v2 of the ring O, when ∠AOO'=α is
Step by step video & image solution for Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v_(1), then velocity v_(2) of the ring O, when /_AOO'=alpha is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
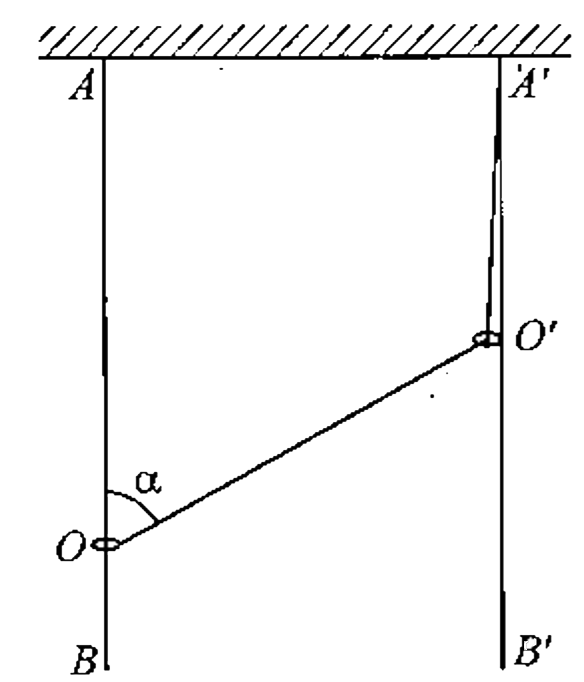
Two rings O and O' are put on two vertical stationary rods AB and A'B' respectively as shown in figure. An inextensible string is fixed at point A' and on ring O and is passed through O' moves downwards at a constant speed v, find the velocity of the ring O in terms of α.
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
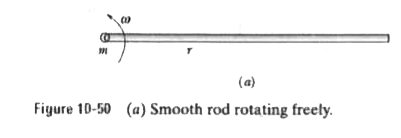
View Solution
Knowledge Check
Two small rings O and O' are put on two vertical stationery rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O.
Assuming that ring O' moves downwards at a constant velocity v1, determine the velocity v2 of the ring O, when ∠AOO'=α.
 Av1[2sin2α/2cosα]Bv1[2cos2α/2sinα]Cv1[3cos2α/2sinα]DNone of these
Av1[2sin2α/2cosα]Bv1[2cos2α/2sinα]Cv1[3cos2α/2sinα]DNone of theseThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
Aπ23B2π23C4π23D8π23A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 AvRB2vRCv2RD3vR
AvRB2vRCv2RD3vR
A ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
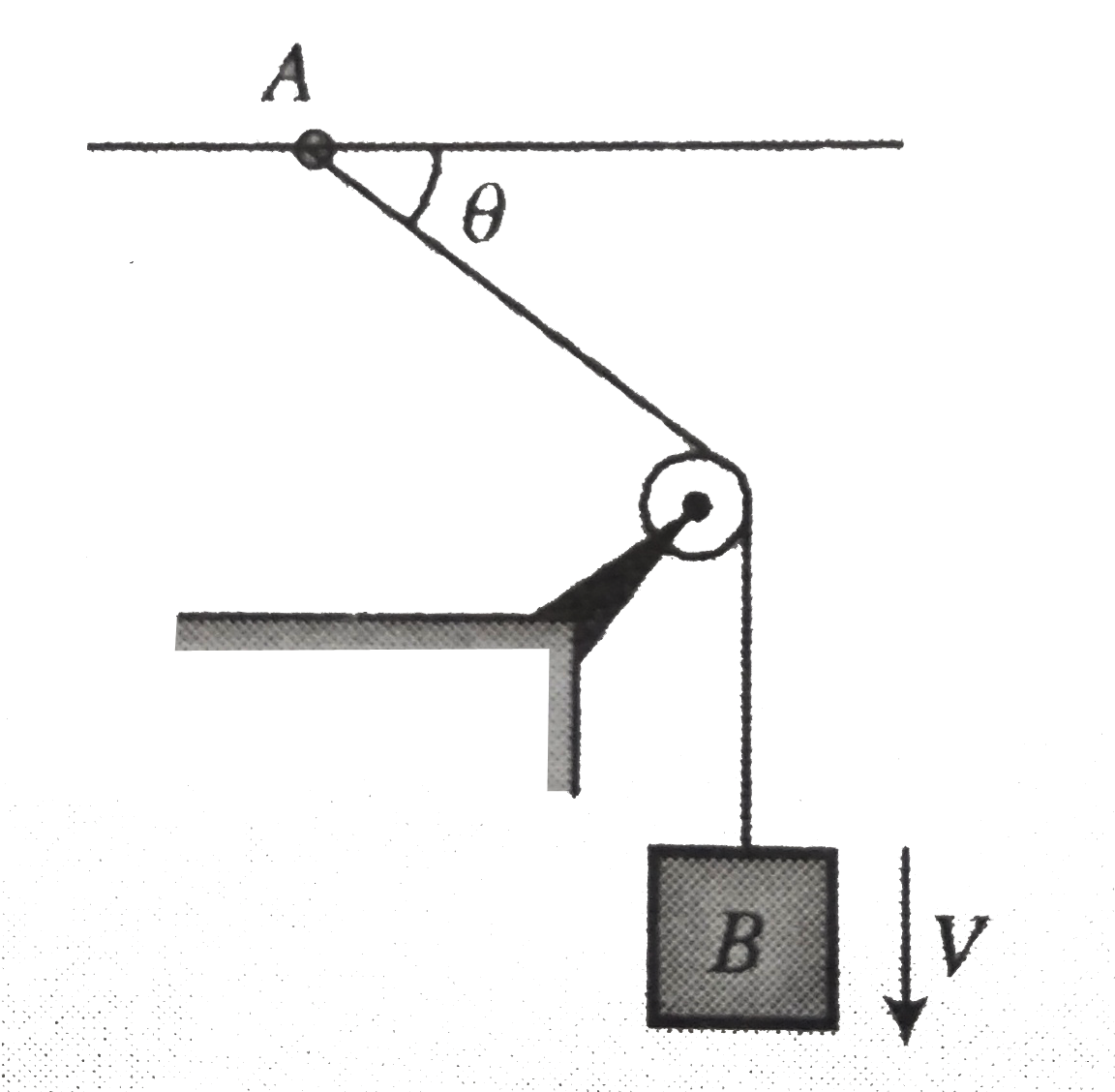
View SolutionA uniform conducting wire is used to make a ring and its two diameters AB and CD. The ring is placed in a uniform magnetic field B perpendicular to its plane. The resistance of the wire per unit length is λΩ/m.
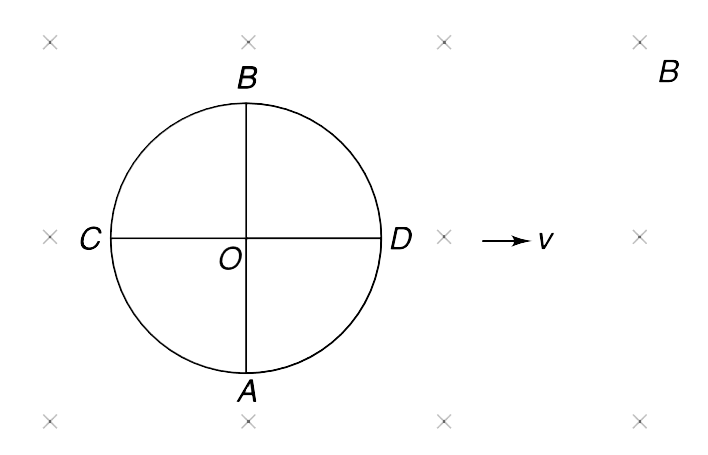
(a) Find the current in BO and BC when the ring is moved with constant velocity v in its plane.
(b) Find current in BO and BC when the ring is kept stationary but the magnetic field is increased at a constant rate of dBDt=αT/s. Assume that magnetic field is confined inside the circular ring only. Take radius of the ring to be a.
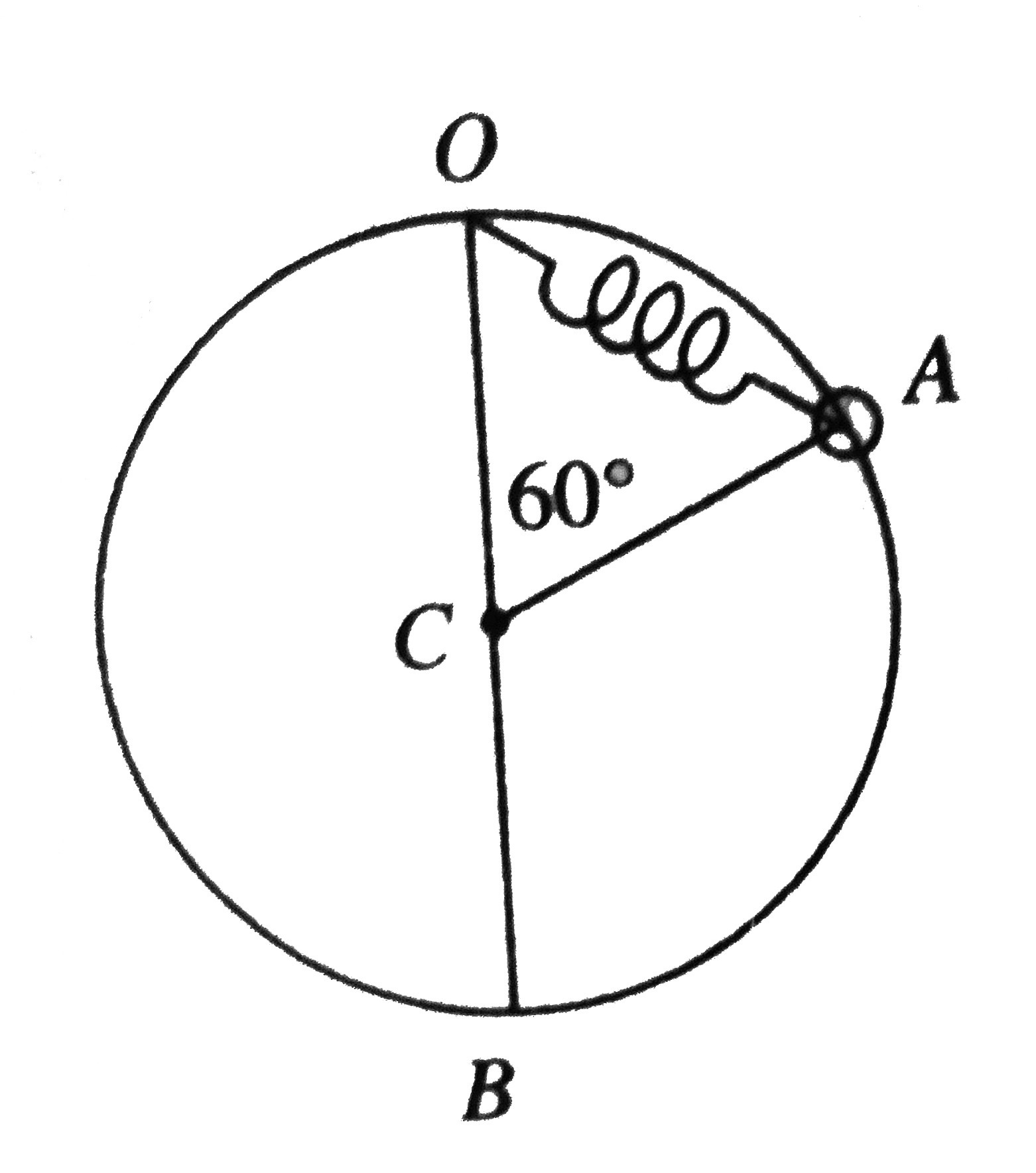
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)

View SolutionA particle is moving in a straight line and passes through a point O with a velocity of 6ms−1 The particle moves with a constant retardation of 2ms−2 for 4 s and there after moves with constant velocity. How long after leaving O does the particle return to O
View Solution
