Two small spheres of masses m1 and m2 are connected by a light right rod.The system is placed between a rought floor and smooth verticle wall as shown in Fig. The co-efficent of friction between the floor and the sphere of mass m2 isμ .Find the minimum value of θ so that the system of masses does not slip

For the equation of m1
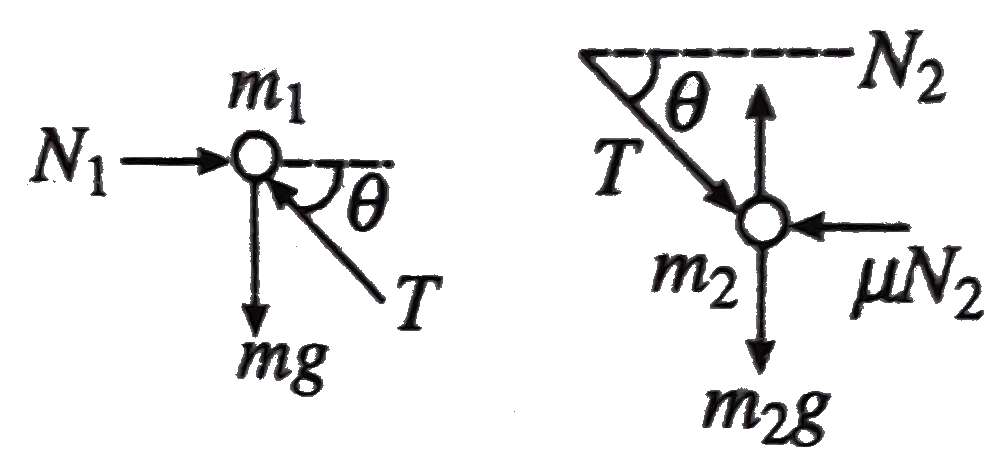
∑Fx=0⇒N1−Tcosθ=0
⇒N1=Tcosθ
∑Fx=0⇒Tsinθ−m1g=0 …(i)
Tsinθ=m2g …(ii)
For the equilibrium of m2
∑Fx=0⇒Tcosθ−μN2=0
⇒Tcosθ=μN2 ....(iii)
∑Fx=0⇒N2−Tsinθ−m2g=0
⇒N2=Tsinθ+m2g ...(iv)
(ii) + (iv) ⇒N2=(m1+m2)g
substituting N2 from (v) in (iii) we obtain
Tcosθ=μ(m1+m2g ....(vi)
(ii) + (vi) tanθ=m1μ(m1+m2)⇒θ=cot−1[μ(1+m1m2)]
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
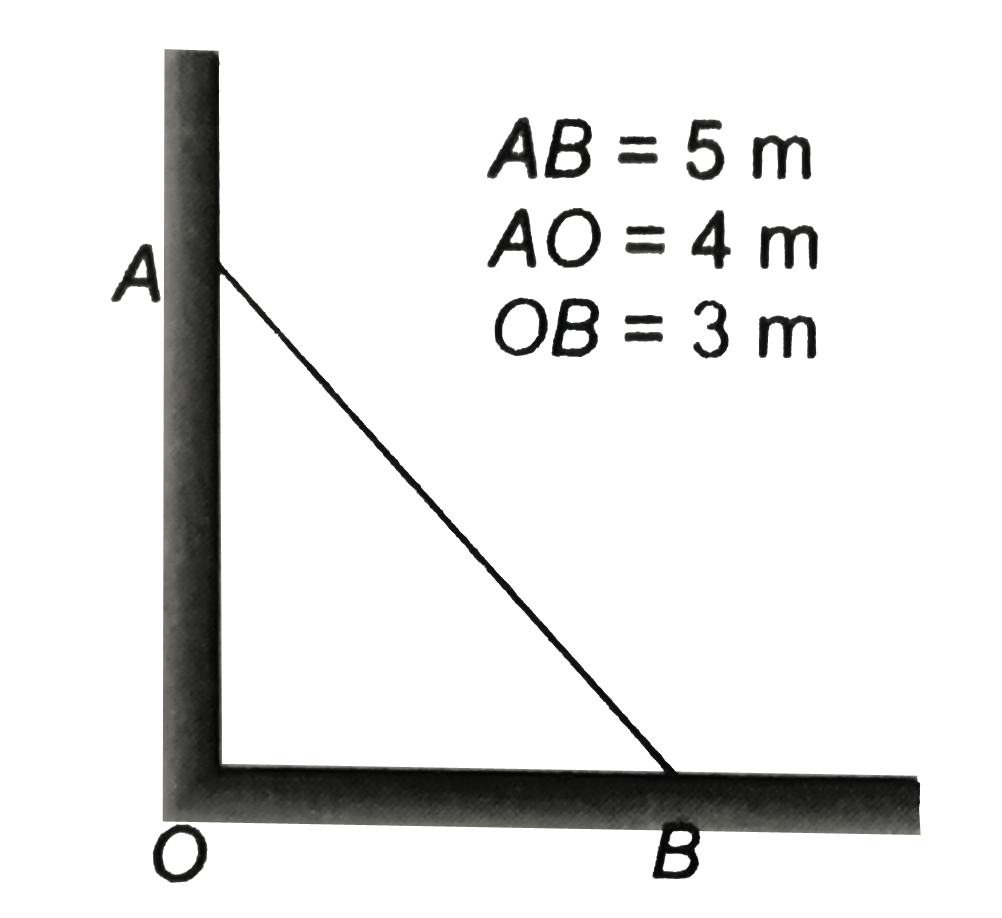
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?

View SolutionIf the coefficient of friction between M and the inclined surfaces is μ=1/√3 find the minimum mass m of the rod so that the of mass M=10kg remain stationary on the inclined plane

View SolutionA mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground

View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo masses M1andM2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system, and the force by the rod on one of the blocks.
View Solution
