Two substances of densities ρ1 and ρ2 are mixed in equal volume and the relative density of mixture is 4. When they are mixed in equal masses, the relative density of the mixture is 3. the values of ρ1 and ρ2 are:
ρ=6 and ρ2=2
ρ3 and ρ2=5
ρ1=12 and ρ2=4
None of these
The correct Answer is:A
To solve the problem, we need to find the densities ρ1 and ρ2 of two substances based on the information provided about their mixtures.
Step 1: Understand the first case (equal volumes)
When the two substances are mixed in equal volumes, the relative density of the mixture is given as 4.
The formula for the density of the mixture when mixed in equal volumes is:
ρmixture=ρ1V+ρ2VV+V=ρ1+ρ22
Given that ρmixture=4:
ρ1+ρ22=4
Multiplying both sides by 2:
ρ1+ρ2=8(Equation 1)
Step 2: Understand the second case (equal masses)
When the substances are mixed in equal masses, the relative density of the mixture is given as 3.
The formula for the density of the mixture when mixed in equal masses is:
ρmixture=m1+m2m1ρ1+m2ρ2
Since m1=m2=m:
ρmixture=m+mmρ1+mρ2=2mmρ1+mρ2=21ρ1+1ρ2
Given that ρmixture=3:
3=21ρ1+1ρ2
Cross-multiplying gives:
3(1ρ1+1ρ2)=2
This simplifies to:
1ρ1+1ρ2=23(Equation 2)
Step 3: Solve the equations
We have two equations now:
1. ρ1+ρ2=8 (Equation 1)
2. 1ρ1+1ρ2=23 (Equation 2)
From Equation 2, we can express it in terms of ρ1 and ρ2:
ρ1+ρ2ρ1ρ2=23
Substituting ρ1+ρ2=8 from Equation 1 into this gives:
8ρ1ρ2=23
Cross-multiplying gives:
8⋅3=2⋅ρ1ρ2
24=2ρ1ρ2
Dividing by 2:
ρ1ρ2=12(Equation 3)
Step 4: Solve the system of equations
Now we have:
1. ρ1+ρ2=8
2. ρ1ρ2=12
Let ρ1 and ρ2 be the roots of the quadratic equation:
x2−(ρ1+ρ2)x+ρ1ρ2=0
This becomes:
x2−8x+12=0
Using the quadratic formula:
x=−b±√b2−4ac2a=8±√64−482=8±√162=8±42
This gives:
x=122=6orx=42=2
Thus, ρ1=6 and ρ2=2 (or vice versa).
Final Answer
The values of ρ1 and ρ2 are:
ρ1=6,ρ2=2
When the two substances are mixed in equal volumes, the relative density of the mixture is given as 4.
ρmixture=ρ1V+ρ2VV+V=ρ1+ρ22
Given that ρmixture=4:
ρ1+ρ22=4
Multiplying both sides by 2:
ρ1+ρ2=8(Equation 1)
When the substances are mixed in equal masses, the relative density of the mixture is given as 3.
ρmixture=m1+m2m1ρ1+m2ρ2
Since m1=m2=m:
ρmixture=m+mmρ1+mρ2=2mmρ1+mρ2=21ρ1+1ρ2
Given that ρmixture=3:
3=21ρ1+1ρ2
Cross-multiplying gives:
3(1ρ1+1ρ2)=2
This simplifies to:
1ρ1+1ρ2=23(Equation 2)
We have two equations now:
1. ρ1+ρ2=8 (Equation 1)
2. 1ρ1+1ρ2=23 (Equation 2)
ρ1+ρ2ρ1ρ2=23
Substituting ρ1+ρ2=8 from Equation 1 into this gives:
8ρ1ρ2=23
Cross-multiplying gives:
8⋅3=2⋅ρ1ρ2
24=2ρ1ρ2
Dividing by 2:
ρ1ρ2=12(Equation 3)
Now we have:
1. ρ1+ρ2=8
2. ρ1ρ2=12
x2−(ρ1+ρ2)x+ρ1ρ2=0
This becomes:
x2−8x+12=0
Using the quadratic formula:
x=−b±√b2−4ac2a=8±√64−482=8±√162=8±42
This gives:
x=122=6orx=42=2
Thus, ρ1=6 and ρ2=2 (or vice versa).
The values of ρ1 and ρ2 are:
ρ1=6,ρ2=2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Equal masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionWhen two substances of specific gravities d1 and d2 are mixed in equal volumes the specific garvity of mixture is found to be ρ1. When they are mixed in equal masses, the specific gravity of the mixture is found to be ρ2.(d1≠d2)
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View Solution
A jar filled with two non-mixing liquid 1 and 2 having densities ρ1 and ρ2 respectively. A solid ball, made of a material of density ρ3 is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for ρ1,ρ2 and ρ3?
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
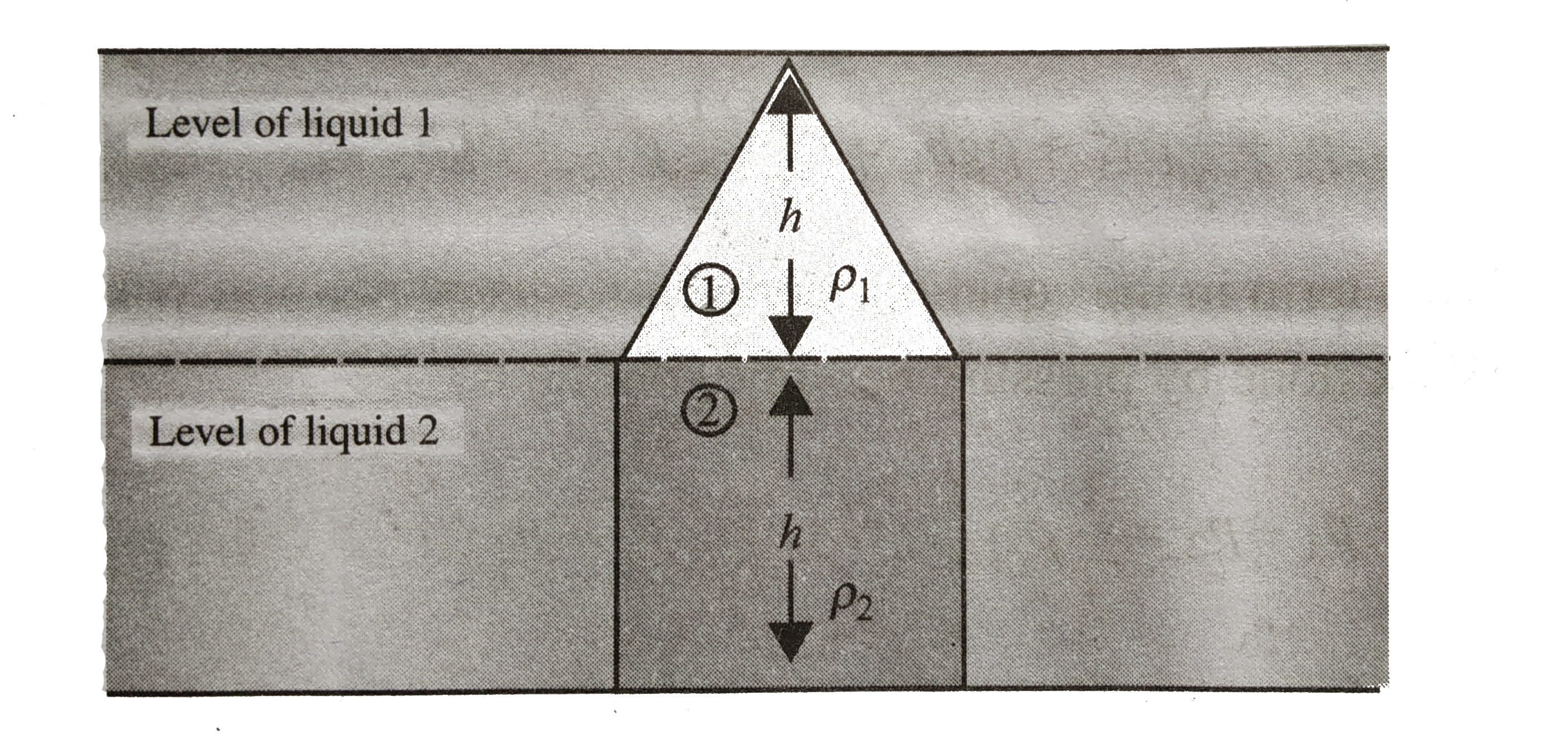
View SolutionA composite plate comprises a triangular area (1) and rectangular area (2) as shown in the figure. The triangular plate experiences forces due to the liquids of densities ρ1 and the rectangular plate experiences the force due to liquid of density ρ2. Find the hydrostatic forces on (a) area 1, (b) area 2, (c) total composite area of the plate. Assume ρ1=ρ and ρ2=2ρ.
View SolutionA rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

View Solution
