Verify the Ampere's law for magnetic field of a point dipole moment $\to M = M ˆ k$ . Take C as the closed curve running clockwise along (i) z-axis from $z = a > 0$ to $z = R$ , (ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane, (iii) along the x-axis from $x = R$ to $x = a$ , and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-y plane.

Text Solution

Verified by Experts

From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment M magnetic field induction at a point direction z from the magnetic dipole of moment is
$[B] = \frac{μ_{0}}{4 π} \frac{2 [M]}{z^{3}} = \frac{μ_{0} M}{2 π z^{3}}$
(i) Along z-axis from P to Q.
$\int_{P}^{Q} B . d i = \int_{P}^{Q} B, d i {cos 0}^{\circ} = \int_{a}^{R} B d z$
$= \int_{a}^{R} \frac{μ_{0}}{2 π} \frac{M}{z^{3}} d z = \frac{μ_{0} M}{2 π} (\frac{- 1}{2}) ⎛ ⎜ ⎝ \frac{1}{R^{2} - \frac{1}{a^{2}}}$
$= \frac{μ_{0} M}{4 π} (\frac{1}{a^{2}} - \frac{1}{B^{2}})$
(ii) Along the quarter circle QS of radius R as given in the figure below

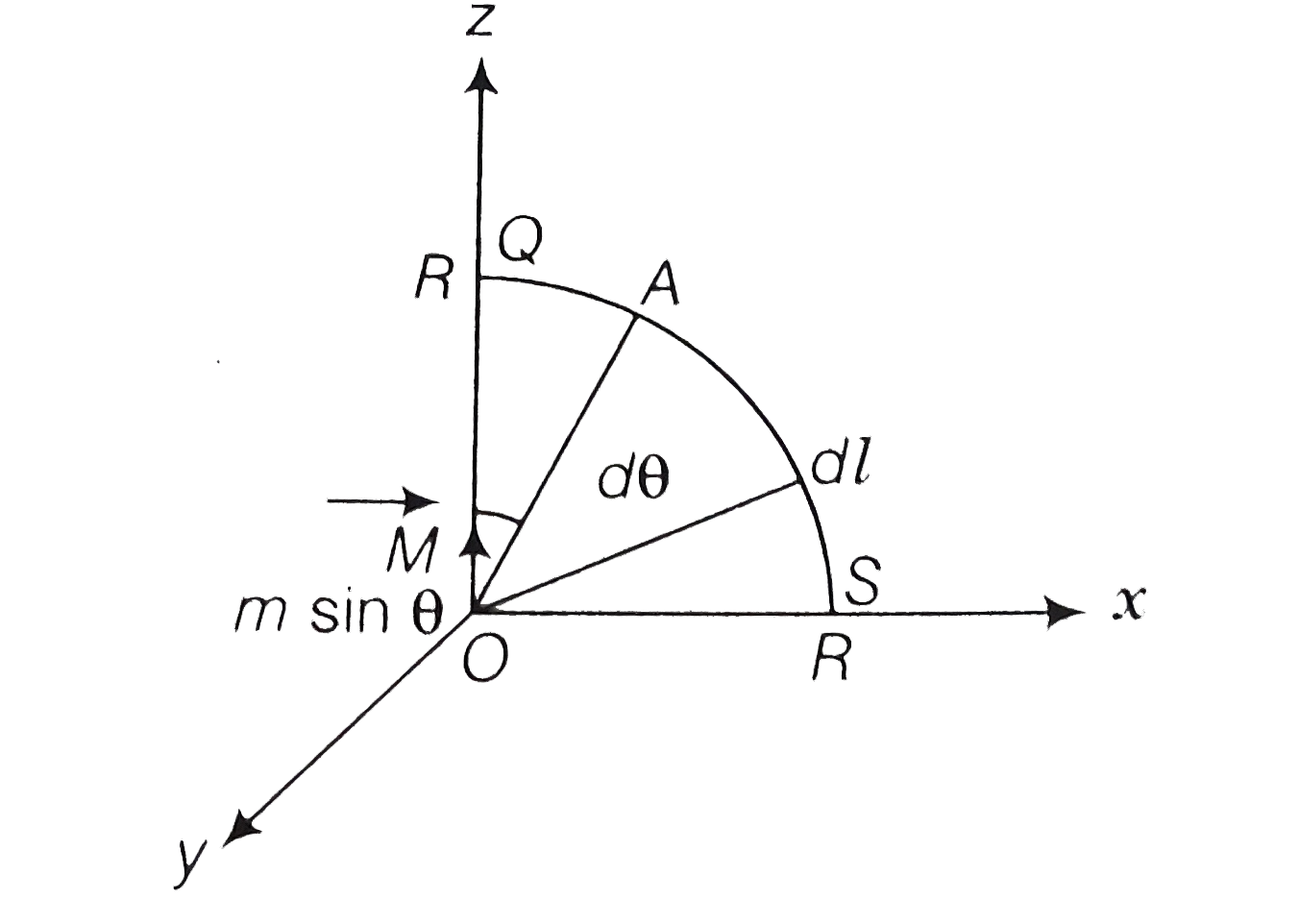
The point A lies on the equational line of the magnetic dipole of moment $M sin θ$ Magnetic field at point A on the circular are is
$B = \frac{μ_{0}}{4 π} \frac{M sin θ}{R^{3}}, d i = R d t h η$
$∴ \int B . d i = \int B, d i cos θ = \int_{Q}^{\frac{π}{2}} \frac{μ_{0}}{4 π} \frac{M sin θ}{R^{3}} R d t h η$
Circular arc $= \frac{μ_{0}}{4 π} \frac{M}{R} {(- cos θ)}_{O}^{π / 2} = \frac{μ_{0}}{4 π} \frac{M}{R^{2}}$
(iii) Along x-axis over the path ST, consider the figure given ahead

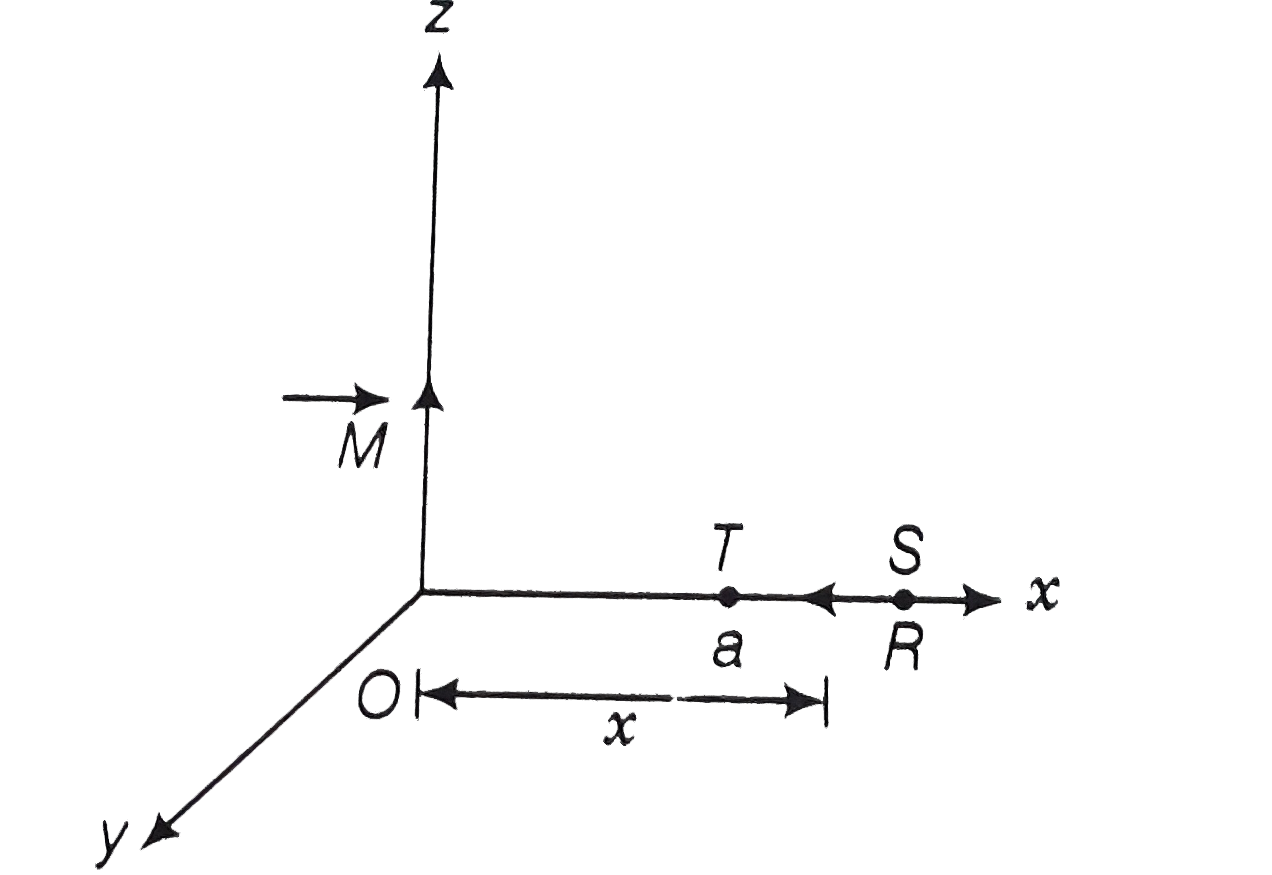
From figure every point lies on the equational line of magnetic dipole Magnetic field induction at a point distance x from the dipole is
$B = \frac{μ_{0}}{4 π} \frac{M}{x^{3}}$
$∴ \int_{S}^{T} B d i = \int_{n}^{a} - \frac{μ_{0} M}{4 π x^{3}} d = 0 [∵ angle between (- M) and d i is 90^{\circ}]$
(iv) Along the quarter circle TP of radius a consider the figure given below

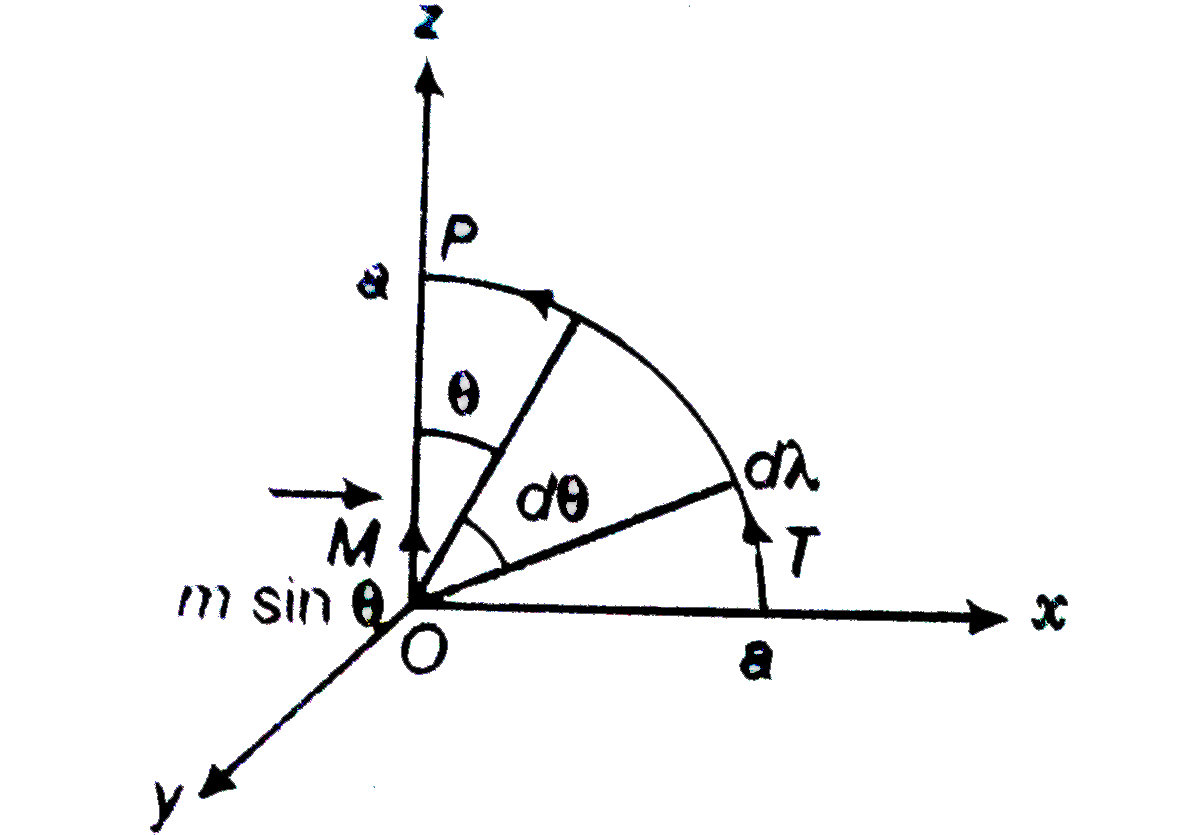
From case (ii), we get the line integral of B along the quarter circle TP of radius a is
Circular arc TP $\int B . d i = \int_{π / 2}^{0} \frac{μ_{0}}{4 π} \frac{M sin θ}{a^{3}} a d t h η$
$= \frac{μ_{0}}{4 π} \frac{M}{a^{2}} {[- cos θ)}_{π / 2}^{0}$
$= \frac{- μ_{0}}{4 π} \frac{M}{a^{2}}$
$∴ \oint B, d i = \int_{P}^{Q} B . d i + \int_{Q}^{S} B . d i + \int_{S}^{T} B . d i + \int_{T}^{P} B . d i$
$= \frac{μ_{0} M}{4} [\frac{1}{a^{2}} - \frac{1}{R^{2}}] + \frac{μ_{0}}{4 π} \frac{M}{R^{2}} + 0 + (- \frac{μ_{0}}{4 π} \frac{M}{a^{2}}) = 0$

Updated on:21/07/2023