Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L>>R, radius of cross-section. In (i) →E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealised assumptions, however, contradict fundamental law as below:
case i contradicts Gauss law for electrostatic fields
case ii contradicts Gauss' law for magnetic fields
case i agrees with ∮E. Dil=0.
case ii contradicts ∮H,dil=Ien
To solve the problem, we need to analyze the two idealized systems mentioned: the parallel plate capacitor and the long solenoid. We will discuss how their ideal assumptions contradict fundamental laws, specifically Gauss's law for electric fields and magnetic fields.
Step 1: Analyze the Parallel Plate Capacitor
- In an ideal parallel plate capacitor, we assume that the electric field (E) between the plates is uniform and constant, and outside the plates, it is zero.
- According to Gauss's law, the electric field E can be expressed as:
∮→E⋅d→A=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
Step 2: Apply Gauss's Law to the Capacitor
- If we consider a Gaussian surface between the plates, there is no charge enclosed (since the charge resides on the plates), thus:
Qenc=0⟹∮→E⋅d→A=0
- This implies that the integral of the electric field over the surface is zero, which contradicts the assumption that E is constant between the plates.
Step 3: Analyze the Long Solenoid
- For the long solenoid, we assume that the magnetic field (B) inside the solenoid is uniform and constant, and outside it is zero.
- According to Gauss's law for magnetism, we have:
∮→B⋅d→A=0
which states that there are no magnetic monopoles.
Step 4: Apply Gauss's Law to the Solenoid
- If we consider a Gaussian surface inside the solenoid, the magnetic field is constant, and we can express the integral as:
B⋅A=0
where A is the area of the Gaussian surface. However, outside the solenoid, the magnetic field is assumed to be zero, which again contradicts the fact that magnetic field lines must form closed loops.
Conclusion:
- Both idealized assumptions contradict fundamental laws:
- The parallel plate capacitor violates Gauss's law for electric fields since it assumes a constant electric field with no enclosed charge.
- The long solenoid violates Gauss's law for magnetism since it assumes a constant magnetic field with no magnetic monopoles.
- In an ideal parallel plate capacitor, we assume that the electric field (E) between the plates is uniform and constant, and outside the plates, it is zero.
- According to Gauss's law, the electric field E can be expressed as:
∮→E⋅d→A=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
- If we consider a Gaussian surface between the plates, there is no charge enclosed (since the charge resides on the plates), thus:
Qenc=0⟹∮→E⋅d→A=0
- This implies that the integral of the electric field over the surface is zero, which contradicts the assumption that E is constant between the plates.
- For the long solenoid, we assume that the magnetic field (B) inside the solenoid is uniform and constant, and outside it is zero.
- According to Gauss's law for magnetism, we have:
∮→B⋅d→A=0
which states that there are no magnetic monopoles.
- If we consider a Gaussian surface inside the solenoid, the magnetic field is constant, and we can express the integral as:
B⋅A=0
where A is the area of the Gaussian surface. However, outside the solenoid, the magnetic field is assumed to be zero, which again contradicts the fact that magnetic field lines must form closed loops.
- Both idealized assumptions contradict fundamental laws:
- The parallel plate capacitor violates Gauss's law for electric fields since it assumes a constant electric field with no enclosed charge.
- The long solenoid violates Gauss's law for magnetism since it assumes a constant magnetic field with no magnetic monopoles.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
Similar Questions
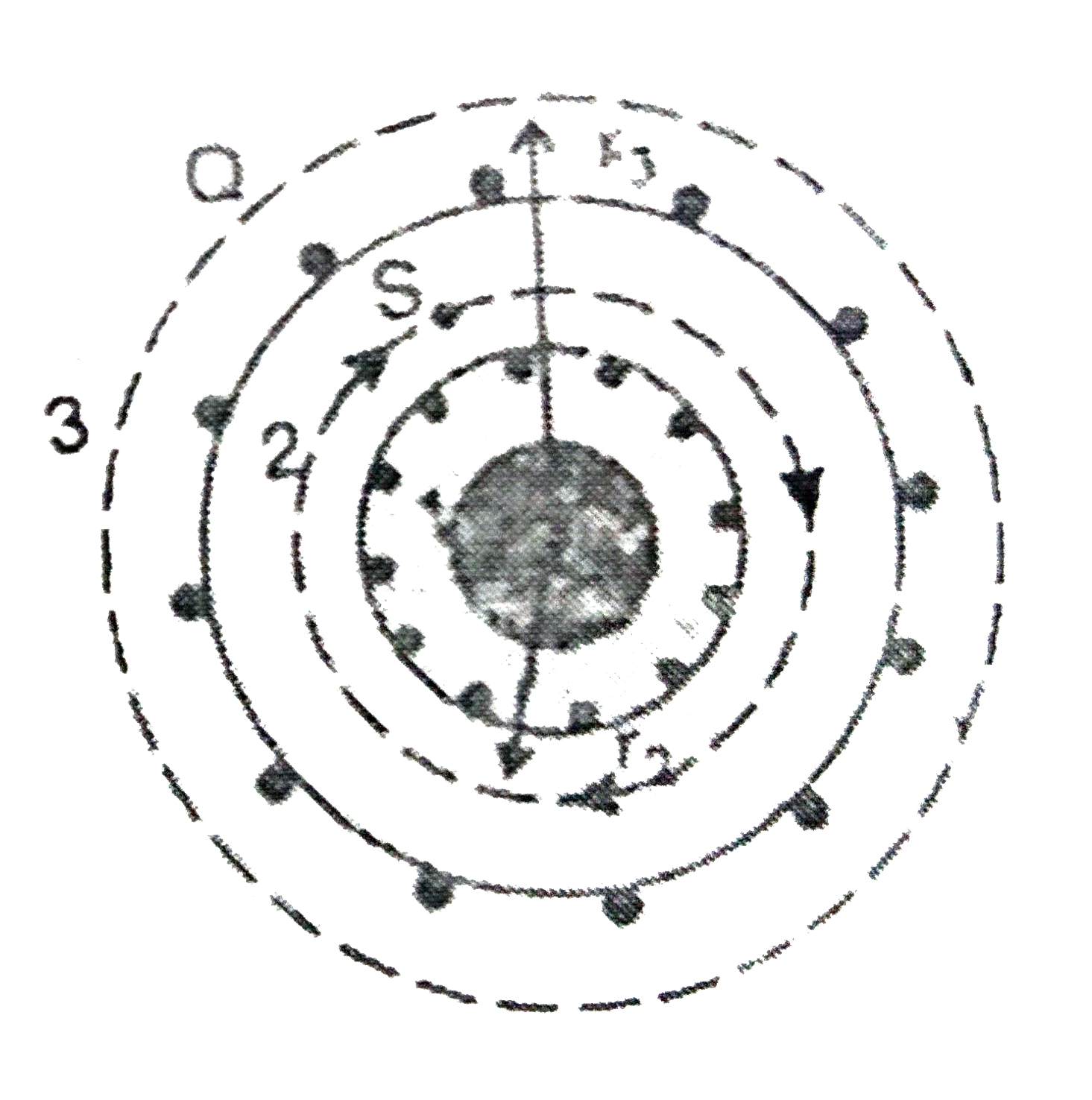
(a) How is a toroid different from a solenoid?
(b) Show that in an ideal toroid, the magnetic field (i) inside the toroid and (ii) outside the toroid at any point in the open space is zero.
 View Solution
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionA parallel plate capacitor each with plate area A and separation ‘d’ is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
(i) charge on the plates
(ii) electric field intensity between the plates,
(iii) capacitance of the capacitor
Justify your answer in each caseView SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
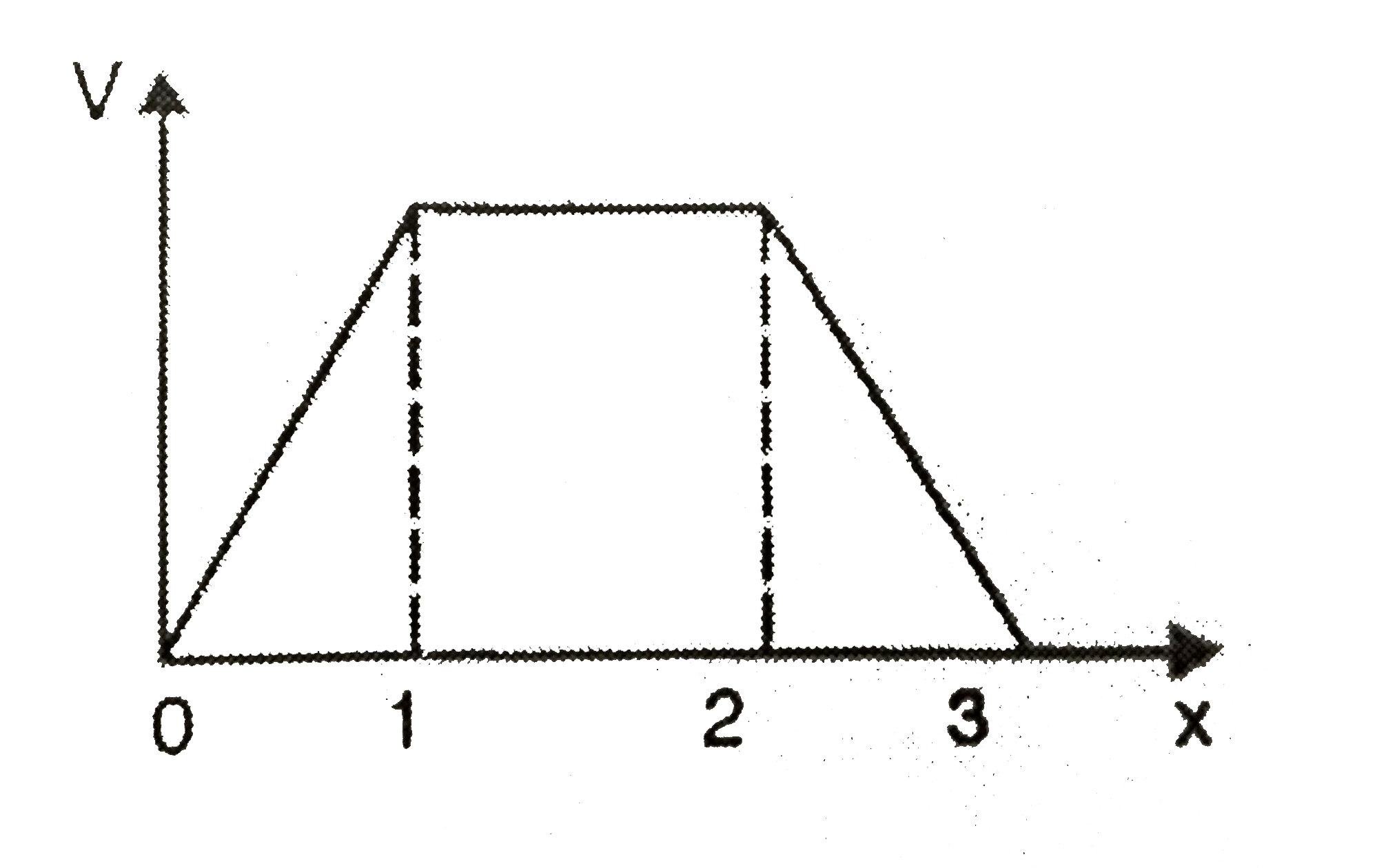
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
 View Solution
View SolutionAn isolated 16μF parallel plate air capacitor has a potential difference of 100 V. dielectric slab having relative permittivity (i.e., dielectric constant) = 5 is introduced to fill the space between the two plates completely. Calculate.
(i) the new capacitance of the capacitor
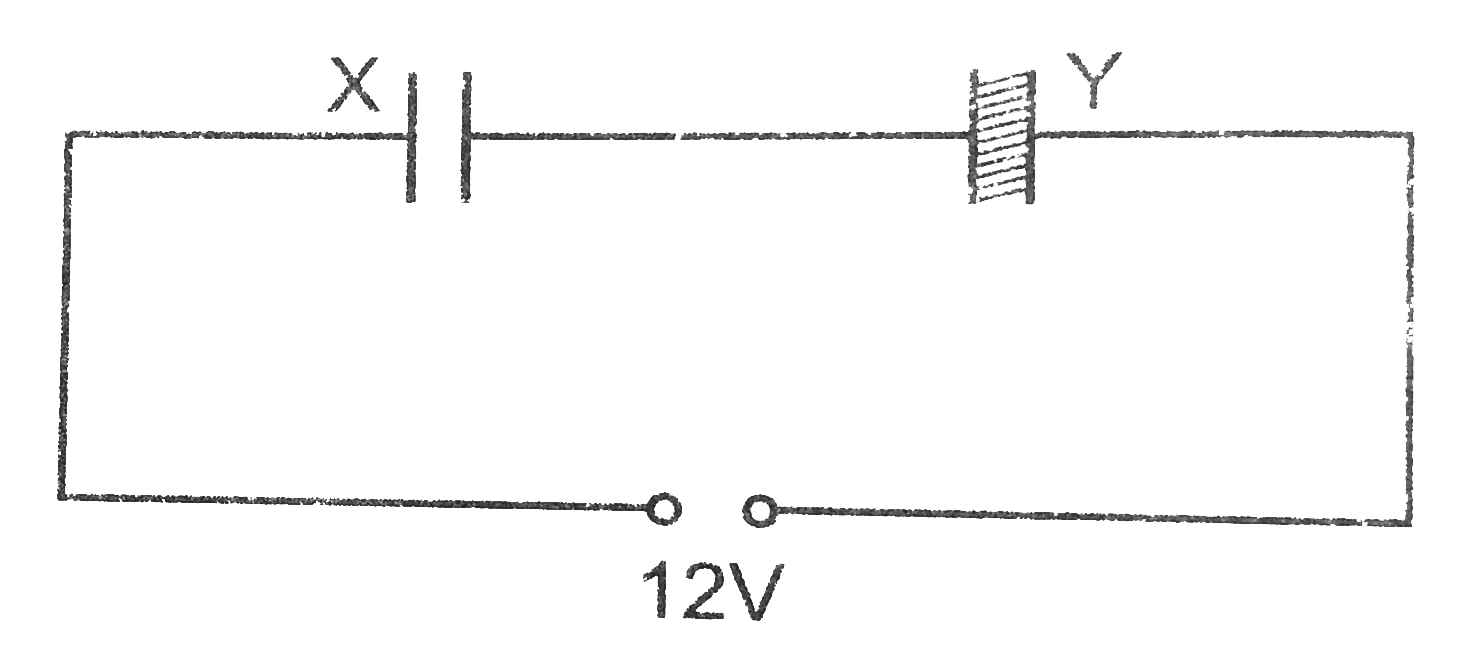
(ii) the new potential differece between the two plates of capacitor.View SolutionTwo parallel palate capacitors X and Y have the same area of plates and same separation between then. X has air between the plates and Y contains a dielectric medium of ∈r=4,
Calculate (i) capacitance of X and Y if equivalent capacitance fo combination is 4μF. (ii) potential diff between the plates of X and Y. (iii) What is the ratio of electrostatic energy stored in X and Y ?
 View Solution
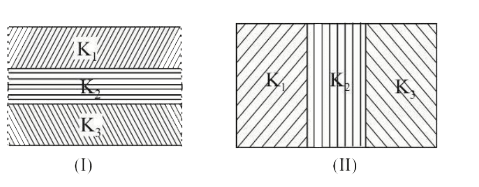
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
 View Solution
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3.
The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II.
If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be ( E1 refers to capacitor (I) and E2 to capacitor (II)):
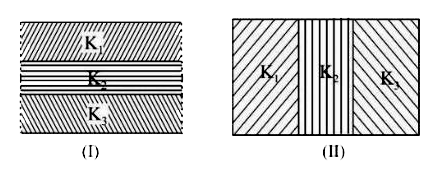 View Solution
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them.
X has air between the plates while Y contains a dielectric medium of er=4
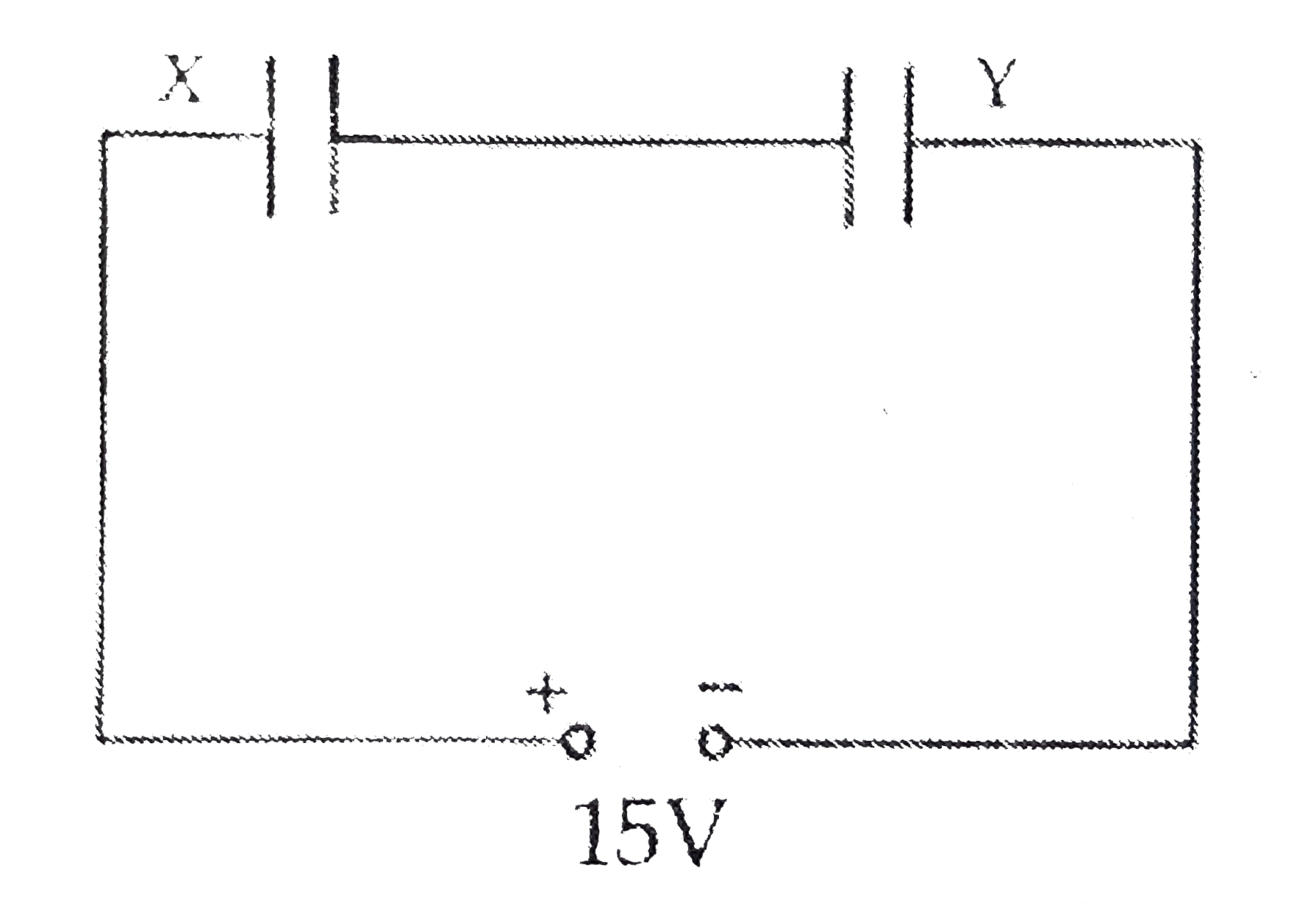
(i) Calculate capacitance of aech capacitor if equivalent capacitance of the combination is 4μF
(ii) Calculate the potential difference between the plates of X and Y
(iii) Estimate the ratio of electrostatic energy stored in X and Y .View SolutionAnswer the following:
(i) If two similar large plates, each of area A having surface charge densities +σ and −σ are separated by a distance d in air,find the expression for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, in which direction will the charge flow and why ?View Solution

