What is the moment of inertia of a ring about a tangent to the circle of the ring ?
To find the moment of inertia of a ring about a tangent to the circle of the ring, we can follow these steps:
Step 1: Understand the Moment of Inertia about the Center
The moment of inertia I of a ring of mass M and radius R about an axis passing through its center and perpendicular to its plane is given by:
Icenter=MR2
Step 2: Apply the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (Z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (X and Y) in the plane of the body:
IZ=IX+IY
For a ring, by symmetry, we have:
IX=IY
Thus, we can express IZ as:
IZ=2IY
Substituting IZ=MR2:
MR2=2IY⟹IY=MR22
Step 3: Apply the Parallel Axis Theorem
Now, we need to find the moment of inertia about an axis that is tangent to the ring. The parallel axis theorem states:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass, and d is the distance from the center of mass to the new axis.
In this case, the distance d from the center of the ring to the tangent is equal to the radius R:
Itangent=IY+MR2
Substituting IY=MR22:
Itangent=MR22+MR2
Step 4: Simplify the Expression
Combining the terms gives:
Itangent=MR22+2MR22=3MR22
Conclusion
The moment of inertia of a ring about a tangent to the circle of the ring is:
Itangent=3MR22
---
The moment of inertia I of a ring of mass M and radius R about an axis passing through its center and perpendicular to its plane is given by:
Icenter=MR2
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (Z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (X and Y) in the plane of the body:
IZ=IX+IY
For a ring, by symmetry, we have:
IX=IY
Thus, we can express IZ as:
IZ=2IY
Substituting IZ=MR2:
MR2=2IY⟹IY=MR22
Now, we need to find the moment of inertia about an axis that is tangent to the ring. The parallel axis theorem states:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass, and d is the distance from the center of mass to the new axis.
Itangent=IY+MR2
Substituting IY=MR22:
Itangent=MR22+MR2
Combining the terms gives:
Itangent=MR22+2MR22=3MR22
The moment of inertia of a ring about a tangent to the circle of the ring is:
Itangent=3MR22
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
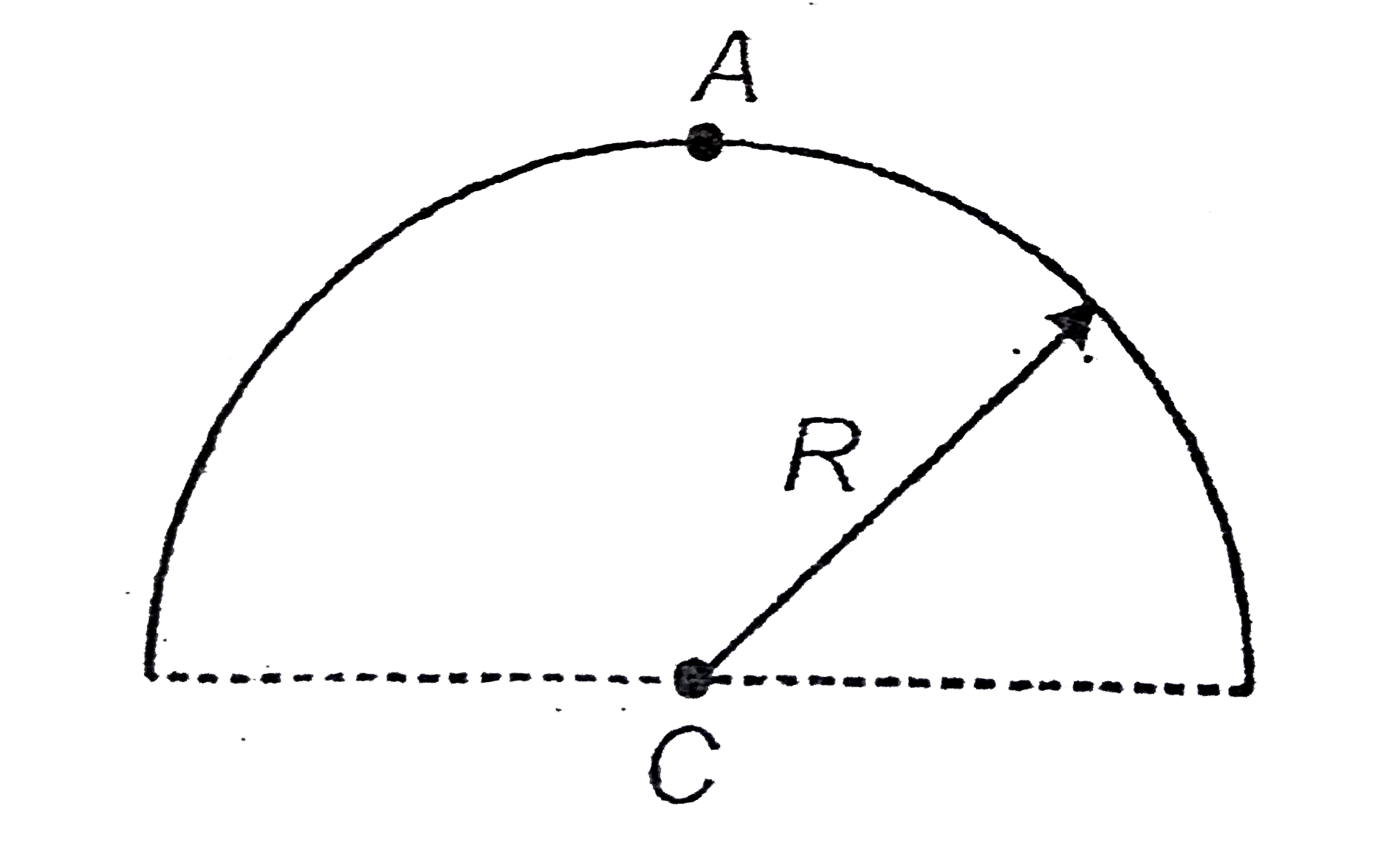
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is IA. If IC is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C, then
View SolutionThe moment of inertia of a ring about an axis passing though the centre and perpendicular to its plane is l. It is rotating ring is gently placed ω Another identical ring is gently placed on it, so that their centres coincide. If both the rings are rotating about the same axis, then loss in kinetic energy is
View SolutionMoment of inertia of a disc about an axis which is tangent and parallel to its plane is I . Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View Solution
