When a man moves down the inclined plane with a constant speed 5ms−1 which makes an angle of 37∘ with the horizontal, he finds that the rain is falling vertically downward. When he moves up the same inclined plane with the same speed, he finds that the rain makes an angle θ=tan−1(78) with the horizontal. The speed of the rain is
√116ms−1
√32ms−1
5ms−1
√73ms−1
The correct Answer is:A, B
To find the speed of the rain, we can break down the problem into steps based on the information given in the question.
1. Understanding the Situation:
- The man moves down the inclined plane at a speed of 5m/s and sees the rain falling vertically.
- When moving up the incline at the same speed, he sees the rain making an angle θ=tan−1(7/8) with the horizontal.
2. Setting Up the Coordinate System:
- Let the velocity of the rain be represented as →vr=a^i+b^j, where a is the horizontal component and b is the vertical component of the rain's velocity.
3. Analyzing the First Case (Moving Down):
- When the man is moving down, his velocity can be broken into components:
Vm=5m/s at 37∘
- The horizontal component Vmx=5cos(37∘)=5⋅45=4m/s
- The vertical component Vmy=5sin(37∘)=5⋅35=3m/s
- The man's velocity vector when moving down the incline is:
→Vm=4^i+3^j
- Since the rain appears to fall vertically, the horizontal component of the rain's velocity relative to the man must be zero:
a−4=0⟹a=4
4. Analyzing the Second Case (Moving Up):
- When the man moves up the incline, his velocity vector is:
→Vm=−4^i−3^j
- The relative velocity of the rain with respect to the man is:
→Vrm=→Vr−→Vm=(a+4)^i+(b+3)^j
- The angle θ formed by the rain with the horizontal is given by:
tan(θ)=vertical componenthorizontal component=b+3a+4
- Given tan(θ)=78:
b+3a+4=78
5. Substituting Known Values:
- We already found a=4:
b+34+4=78
b+38=78⟹b+3=7⟹b=4
6. Finding the Speed of the Rain:
- Now we have a=4 and b=4. The speed of the rain can be calculated using the Pythagorean theorem:
vr=√a2+b2=√42+42=√16+16=√32=4√2m/s
Final Answer:
The speed of the rain is 4√2m/s.
- The man moves down the inclined plane at a speed of 5m/s and sees the rain falling vertically.
- When moving up the incline at the same speed, he sees the rain making an angle θ=tan−1(7/8) with the horizontal.
- Let the velocity of the rain be represented as →vr=a^i+b^j, where a is the horizontal component and b is the vertical component of the rain's velocity.
- When the man is moving down, his velocity can be broken into components:
Vm=5m/s at 37∘
- The horizontal component Vmx=5cos(37∘)=5⋅45=4m/s
- The vertical component Vmy=5sin(37∘)=5⋅35=3m/s
→Vm=4^i+3^j
a−4=0⟹a=4
- When the man moves up the incline, his velocity vector is:
→Vm=−4^i−3^j
→Vrm=→Vr−→Vm=(a+4)^i+(b+3)^j
tan(θ)=vertical componenthorizontal component=b+3a+4
- Given tan(θ)=78:
b+3a+4=78
- We already found a=4:
b+34+4=78
b+38=78⟹b+3=7⟹b=4
- Now we have a=4 and b=4. The speed of the rain can be calculated using the Pythagorean theorem:
vr=√a2+b2=√42+42=√16+16=√32=4√2m/s
The speed of the rain is 4√2m/s.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30∘ with the vertical . Find the speed of the rain drops ( in km/h)
View SolutionA man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60∘ with the horizontal. The velocity of rain with respect to running man is
View SolutionA stationary man observes that the rain is falling vertically downwards. When he starts running a velocity of 12kmh−1, he observes that the rain is falling at an angle 60∘ with the vertical. The actual velocity of rain is
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View SolutionA man is running up an inclined plane ( making an angle θ with the horizontal ) with a speed u. Rain drops falling at an angle α with the vertical appear to the man as if they are falling at an angle of 45∘ with the horizontal . The speed of the rain drops is
View SolutionA block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
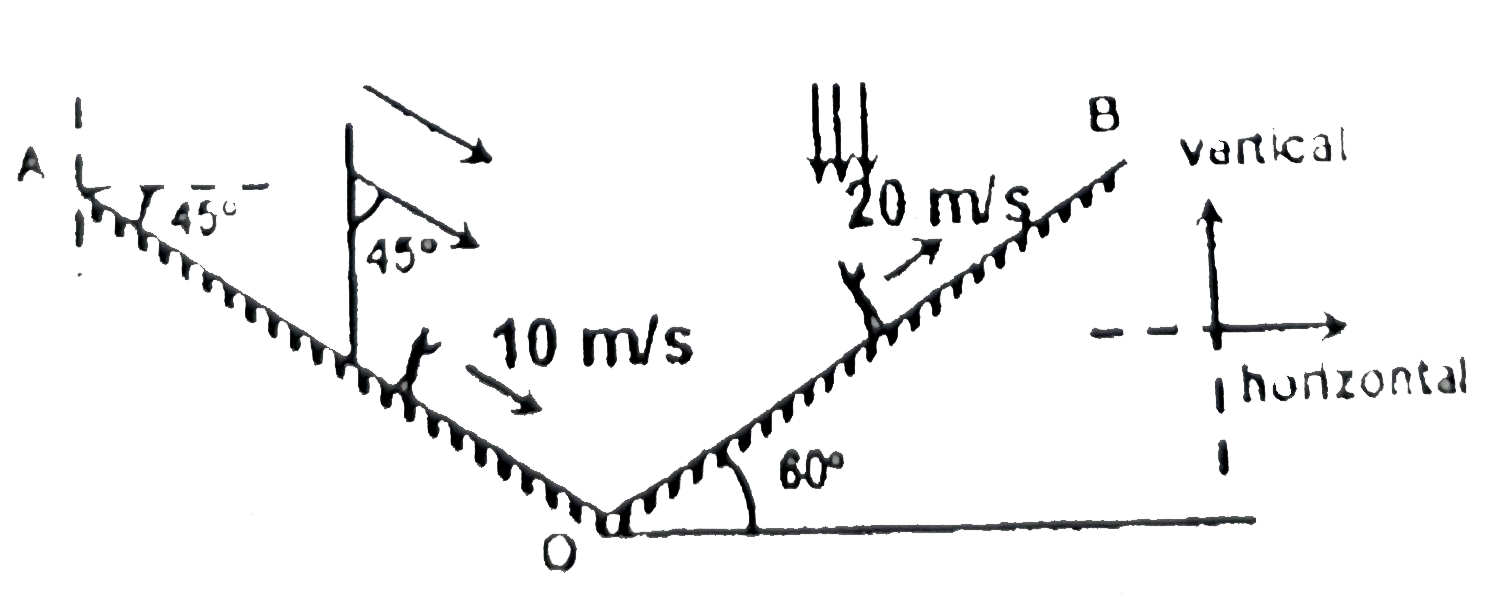
View SolutionThere are two incline planes AO and OB inclined at 45∘ and 60∘ respectively with the horizontal as shown in the figure. When a man moves on the inclined plane AO he is oberves that the rain drops are falling 45∘ with the vertical. When the man moves on the inclined plane OB, he observes that the raindrops are falling vertically downward with the horizontal. Then actual speed of rain is
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
View Solution
