When the switch is open in lowerpoint loop of a potentiometer, the balance point length is 60cm. When the switch is closed with a known resistance of R=4Ω the balance point length decreases to 40cm. Find the internal resistance of the unknown battery.
To solve the problem, we will use the principles of a potentiometer and Ohm's law. Here’s a step-by-step solution:
Step 1: Understand the Setup
When the switch is open, the balance point is at 60 cm. This means the potential difference across this length is equal to the EMF (E) of the unknown battery. When the switch is closed, the balance point changes to 40 cm.
Step 2: Write the Equations for Each Case
1. When the switch is open:
E=k⋅60(where k is the potential gradient)
2. When the switch is closed:
The potential difference across the length of 40 cm is given by:
VPQ=I⋅R
where I is the current flowing through the circuit and R is the known resistance (4 Ω).
Step 3: Calculate the Current
Using Ohm's law, the current I can be expressed as:
I=Er+R
where r is the internal resistance of the unknown battery.
Step 4: Substitute the Current into the Second Equation
Substituting the expression for I into the equation for VPQ:
VPQ=Er+R⋅R
This potential difference is also equal to the potential across the 40 cm length:
k⋅40
Step 5: Set Up the Ratio of the Two Cases
From the two equations we have:
1. E=k⋅60
2. Er+R⋅R=k⋅40
Now, we can divide the two equations:
EEr+R⋅R=6040
This simplifies to:
(r+R)R=6040=32
Step 6: Solve for Internal Resistance r
From the equation:
r+RR=32
Cross-multiplying gives:
2(r+R)=3R
Expanding and rearranging:
2r+2R=3R⟹2r=R⟹r=R2
Substituting R=4Ω:
r=42=2Ω
Final Answer
The internal resistance of the unknown battery is r=2Ω.
---
When the switch is open, the balance point is at 60 cm. This means the potential difference across this length is equal to the EMF (E) of the unknown battery. When the switch is closed, the balance point changes to 40 cm.
1. When the switch is open:
E=k⋅60(where k is the potential gradient)
2. When the switch is closed:
The potential difference across the length of 40 cm is given by:
VPQ=I⋅R
where I is the current flowing through the circuit and R is the known resistance (4 Ω).
Using Ohm's law, the current I can be expressed as:
I=Er+R
where r is the internal resistance of the unknown battery.
Substituting the expression for I into the equation for VPQ:
VPQ=Er+R⋅R
This potential difference is also equal to the potential across the 40 cm length:
k⋅40
From the two equations we have:
1. E=k⋅60
2. Er+R⋅R=k⋅40
EEr+R⋅R=6040
This simplifies to:
(r+R)R=6040=32
From the equation:
r+RR=32
Cross-multiplying gives:
2(r+R)=3R
Expanding and rearranging:
2r+2R=3R⟹2r=R⟹r=R2
Substituting R=4Ω:
r=42=2Ω
The internal resistance of the unknown battery is r=2Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 1
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 2
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View Solution
Knowledge Check
In a potentiometer the balancing with a cell is at length of 220cm. On shunting the cell with a resistance of 3Ω balance length becomes 130cm. What is the internal resistance of this cell.
A4.5ΩB7.8ΩC6.3ΩD2.08Ω
In the potentiometer circuit shown in the figure the balance length AJ=60cm when switch S is open. When switch S is closed and the value of R=5Ω, the b alance length AJ=50cm. The internal resistance of the cell C' is

View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionA battery is connected to a potentiometer and a balance point is obtained at 84cm along the wire. When its terminals are connected by a 5Ω resistor, the balance point changes to 70cm.
Calculate the internal resistance of the cell.
View Solution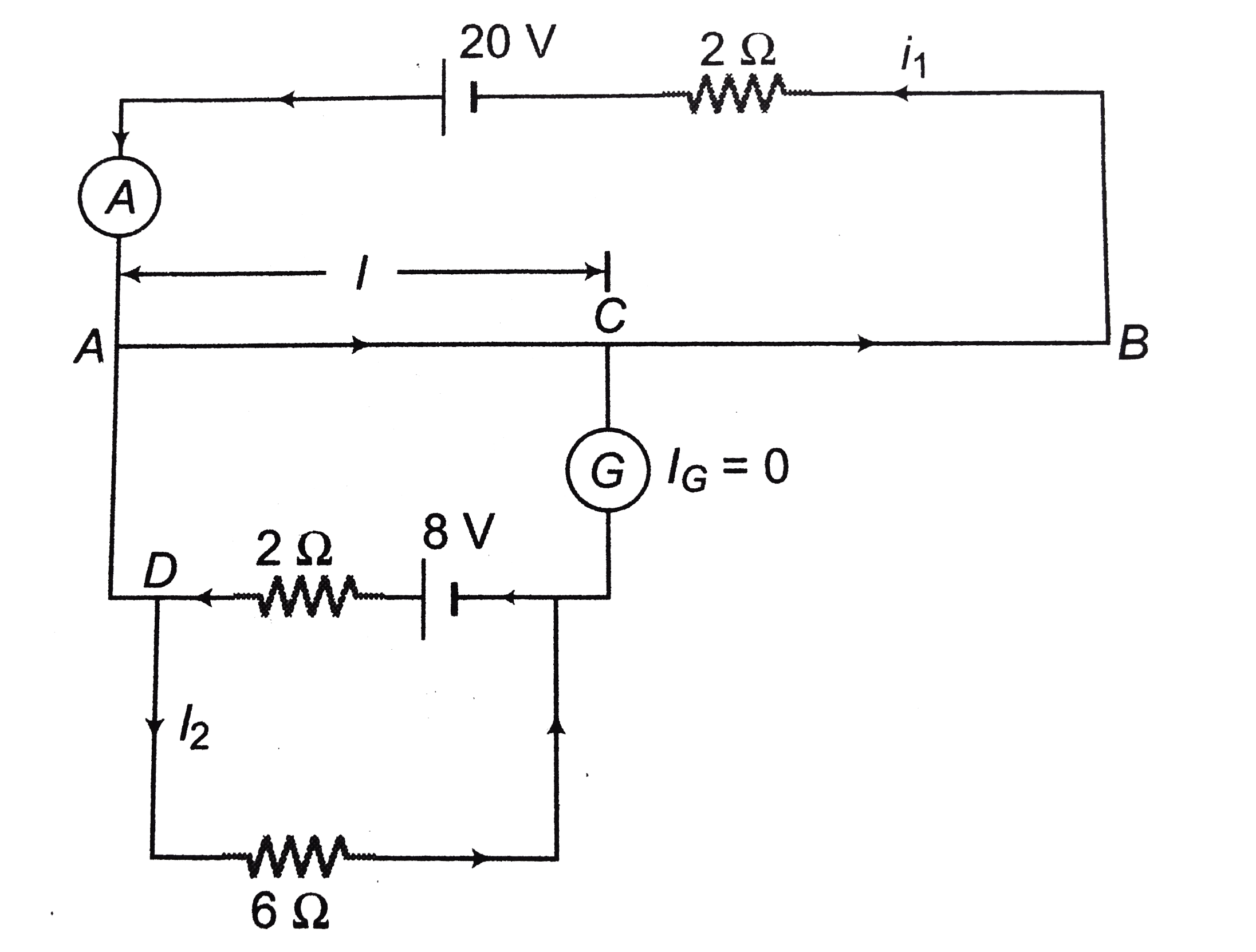
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionIn a potentiometer arrangement for determining the emf of cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9Ω is used in the external circuit of cell , the balance point shifts to 300 cm. Determine the internal resistance of the cell.
View SolutionWhen a Daniel cell is connected in the secondary circuit of a potentiometer, the balancing length is found to be 540 cm. If the balancing length becomes 500 cm. When the cell is short-circuited with 1Ω, the internal resistance of the cell is
View SolutionA battery of unknown emf connected to a potentiometer has balancing length 560 cm. If a resistor of resistance 10 ohm, is connected in parallel with the cell the balancing length change by 60 cm. If the internal resistance of the cell is n10 ohm, the value of 'n' is
View Solution
