Write down the expression for the period of oscillation of a mass attached to (i) a horizontal spring and (ii) a vertical spring.
To derive the expressions for the period of oscillation of a mass attached to both a horizontal spring and a vertical spring, we can follow these steps:
(i) Period of Oscillation for a Vertical Spring
1. Identify the System: Consider a mass m attached to a vertical spring with spring constant k. When the mass is attached, it stretches the spring due to the force of gravity.
2. Displacement: Let y be the displacement from the mean position (equilibrium position) along the vertical axis.
3. Restoring Force: The restoring force F exerted by the spring is given by Hooke's law:
F=−ky
The negative sign indicates that the force is in the opposite direction to the displacement.
4. Newton's Second Law: According to Newton's second law, the force can also be expressed as:
F=ma
where a is the acceleration.
5. Acceleration in Terms of Displacement: The acceleration can be expressed as:
a=d2ydt2
Therefore, we can equate the two expressions for force:
md2ydt2=−ky
6. Form the Differential Equation: Rearranging gives us:
d2ydt2+kmy=0
This is a standard form of the simple harmonic motion equation.
7. Identify Angular Frequency: The angular frequency ω is defined as:
ω2=km
8. Relate Angular Frequency to Period: The period T of oscillation is related to angular frequency by:
T=2πω
9. Final Expression for Period: Substituting ω gives:
T=2π√mk
(ii) Period of Oscillation for a Horizontal Spring
1. Identify the System: Consider a mass m attached to a horizontal spring with spring constant k.
2. Displacement: Let x be the displacement from the mean position (equilibrium position) along the horizontal axis.
3. Restoring Force: The restoring force F exerted by the spring is given by Hooke's law:
F=−kx
4. Newton's Second Law: According to Newton's second law, the force can also be expressed as:
F=ma
where a is the acceleration.
5. Acceleration in Terms of Displacement: The acceleration can be expressed as:
a=d2xdt2
Therefore, we can equate the two expressions for force:
md2xdt2=−kx
6. Form the Differential Equation: Rearranging gives us:
d2xdt2+kmx=0
This is also a standard form of the simple harmonic motion equation.
7. Identify Angular Frequency: The angular frequency ω is defined as:
ω2=km
8. Relate Angular Frequency to Period: The period T of oscillation is related to angular frequency by:
T=2πω
9. Final Expression for Period: Substituting ω gives:
T=2π√mk
Summary of Results
- The period of oscillation for both the vertical and horizontal spring systems is given by:
T=2π√mk
F=−ky
The negative sign indicates that the force is in the opposite direction to the displacement.
F=ma
where a is the acceleration.
a=d2ydt2
Therefore, we can equate the two expressions for force:
md2ydt2=−ky
d2ydt2+kmy=0
This is a standard form of the simple harmonic motion equation.
ω2=km
T=2πω
T=2π√mk
F=−kx
F=ma
where a is the acceleration.
a=d2xdt2
Therefore, we can equate the two expressions for force:
md2xdt2=−kx
d2xdt2+kmx=0
This is also a standard form of the simple harmonic motion equation.
ω2=km
T=2πω
T=2π√mk
- The period of oscillation for both the vertical and horizontal spring systems is given by:
T=2π√mk
Topper's Solved these Questions
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - VERY SHORT ANSWER QUESTIONS13videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM THE CHARACTERISTIC OF SHM)14videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS3videos
OSCILLATIONS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS12videos
PROPERTIES OF MATTER
Similar Questions
Write down the expression for the period of oscillation of a light piece of cork floating in a liquid .
View SolutionObtain an expression for the period of oscillations of a mass attached to end of a spring and undergoing shm. Obtain expression for K.E. and P.E. at any position during shm.
View Solution
Knowledge Check
- Question 1 - Select One
If the period of oscillation of mass M suspended. From a spring is one second, then the period of 4 M will be
A1/2B1/4 secC2 secD4 sec
Derive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View SolutionWrite the expression for equivalent spring constant of
(i) parallel combination of n−springs
(ii) series combination of n−springsView SolutionThe time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View SolutionA bar of mass m is suspended horizontally on two vertical springs of spring constant k and 3k. The bar bounces up and down while remaining horizontal. Find the time period of oscillation of the bar neglect mass of springs and friction everywhere
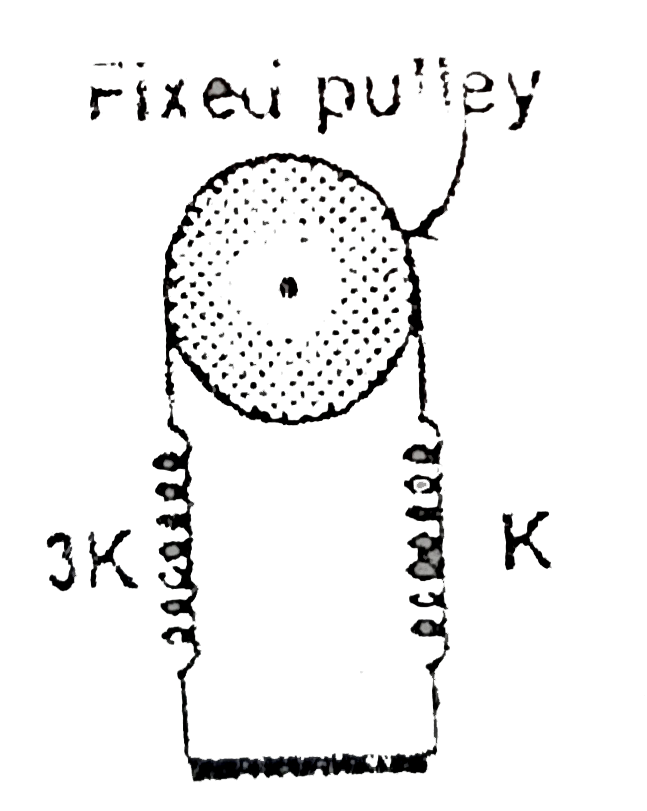 View Solution
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 View Solution
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
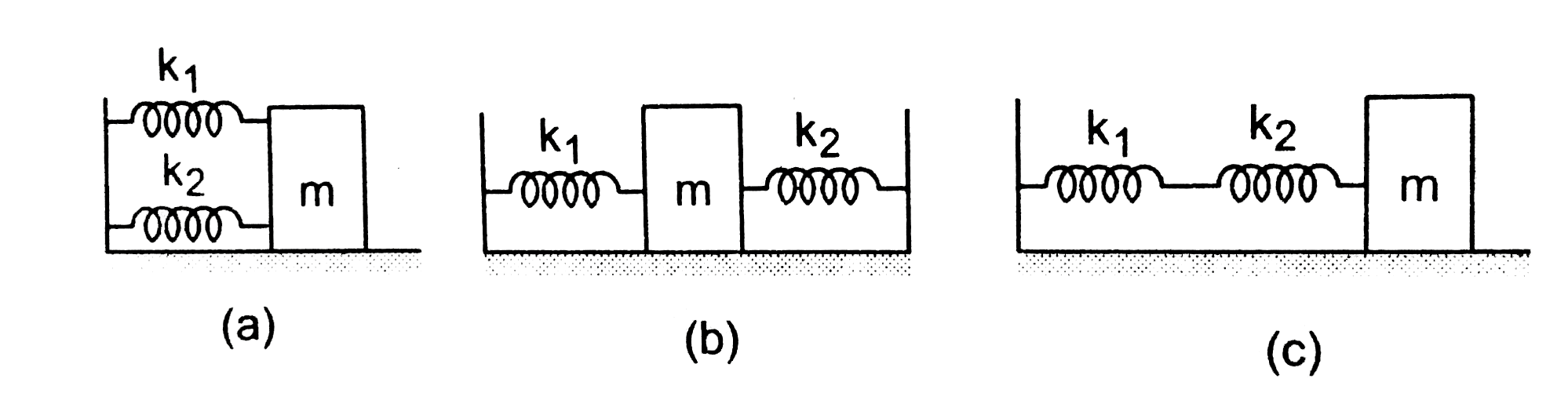 View Solution
View Solution

