Write using Biot-Savart law, the expression for the magnetic field →B due to an element →dl carrying current I at a distance →r from it in vector form. Hence, derive the expression for the magnetic field due to a current loop of radius R at a point P distant x from its centre along the aixs of the loop.
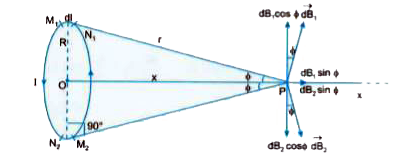
Consider a circular loop of radius R, carrying a current l. Plane of the coil is Y - Z plane (i.e, perpendicular to the plane of paper), while the axis of the loop OX lies in the plane of paper. Consider the circular loop to be divided into large number of current elements I→dl. Two such elements N1M1 and N2M2, diametrically opposite to each other, produce the magnetic fields →dB1 and d→B2 perpendicular to both →r and →dl and given by right hand rule as,
∣∣d→B1∣∣=∣∣d→B2∣∣=μ04π⋅Idlsin90∘r2=μ04πIdl(R2+x2)
These field may be resolved into components along x-aix and y - axis. Obviously components along y-axis balance each other but components along x-axis and y-axis. Obviously components along y-axis balance each other but components along x-axis are all summed up. Hence, magnetic field due to whole current loop will be :
B=∮dBsinϕ=∮μ04πIdl(R2+x2)⋅R√(R2+x2)=μ0IR4π(R2+x2)3/2∮dl
=μ0IR4π(R2+x2)3/2⋅2πR=μ0IR22(R2+x2)3/2
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
(a) Write, using Biot-Savart law, the expression for the magnetic field →B due to an element →dl carrying current I at a distance →r from it in a vector form.
Hence ,derive the expression for the magnetic field due to a current carring loop of radius R at a point P distant x from its centre along the axis of the loop.
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View Solution
Knowledge Check
The magnetic field (d→B) at a point due to an elemental conductor (d→l) carrying a current (i) at a distance (→r) from the elemetn, is given by
AFaraday's LawBColumb's LawCBiot-Savart's LawDAmpere's Law
A circular loop of radius R carries a current I. Obtain an expression for the magnetic field at a point on its axis at a distance x from its centre.
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View SolutionState Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.
View SolutionState the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View SolutionDerive an expression for magnetic field strength B at a point P due to current flowing through a straight conductor using Biot Savart's law.
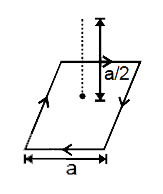
View SolutionThe magnetic field due to a current carrying square loop of side a at a point located symmetrically at a distance of a/2 from its centre (as shown is)
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to circular wire carrying current I.
View Solution
