AB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
Let O is center and r is radius of circle whose chords AB=6cm,CD=12cm.
Draw OM⊥AB which cuts CDat N
AB∣∣CDand ON⊥CD
OM⊥AB,AM=MB(Perpendicular drawn from center of circle bisects the chord.
AM=MB=12AB=12×6=3cm
ON⊥CD
CN=ND=12×CD=12×12=6cm
Distance between chords ABand CDMN=3cm.
Let ON=xcm.
In right angled △OCN, by Pythagoras theorem
OC2=ON2+CN2
(OC)2=(x)2+(6)2
(OC)2=x2+36 …..(i)
Now in right angled △OAM By Pythagoras
OA2=AM2+OM2
OA2=AM2+(ON+MN)2
OA2=AM2+(x+3)2
OA2=(3)2+(x+3)2
OA2=9+x2+9+6x …..(ii)
OA=OC
OA2=OC2
x2+36=9+x2+9+6x(from equation (i) and (ii))
36=6x+18
6x=36–18
6x=18⇒x=186=3cm
Putting value of x in equation in (i),(OC)2=(3)2+36=9+36=45
OC=√45
OC=3√5cm.
Thus, radius of circle is 3√5cm
Topper's Solved these Questions
Similar Questions
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is 6 cm
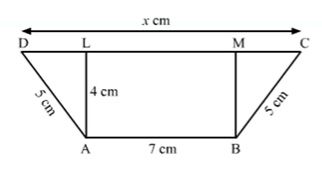
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
 View Solution
View SolutionIn Fig. 10.57, a circle is inscribed in a quadrilateral ABCD in which ∠B=90o . If AD=23cm , AB=29cm and DS=5cm , find the radius r of the circle. (FIGURE)
View SolutionIn Fig.38, ABCD and PQRC are square such that AD=22 cm and PC=y cm. If the area of the shaded region is 403 cm2, then the value of y is (a)3 (b) 6 (c)9 (d) 10
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=6 cm , DB=9 cm and AE=8 cm , find AC . (ii) If ADDB=34 and AC=15 cm , find AE . (iii) If ADDB=23 and AC=18 cm , find AE .
View SolutionIn Fig.85, ABCD and ACBD. Find the value of x,y,z.
View SolutionIn ABC, D, E and F are, respectively, the mid-points of BC, CA and AB . If the lengths of side AB, BC and CA are 7cm, 8cm, and 9cm, respectively, find the perimeter of DEF
View Solution

