are two parallel chords of a circle whose centre is and radius is If find the distance between if they lie: on opposite side of the centre
We join
drop perpendicular from
The perpendiculars meet at respectively.
Since, are perpendiculars to
who are
parallel lines, will be on the same straight line
disance between .........(i)
......(ii)
Again are mid points of respectively.
since
respectively and the perpendicular, dropped from the center of a circle to any of its chord, bisects the latter.
So
are right triangles with as hypotenuses.(from ii)
So, by Pythagoras theorem, we get
Now two cases arise- (i) are to the opposite side of the centre O.
Here, (from i)
(ii) are to the same side of the center O. (fig II)
Here
So the distance between
when are to the opposite side of the centre
the distance between
when are to the same side of the centre
Topper's Solved these Questions
Similar Questions
PQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on the same side of centre O
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is 6 cm
View SolutionLet AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA.PB=9,QC.QD=16, then distance betweẹn AB and CD is
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13cm. A is any point on PQ. If PS=5cm, then find ar(RAS)
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionPQRS is a parallelogram. PXandQY are respectively, the perpendiculars from PandQ to SRandRS produced. Prove that PX=QY
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.
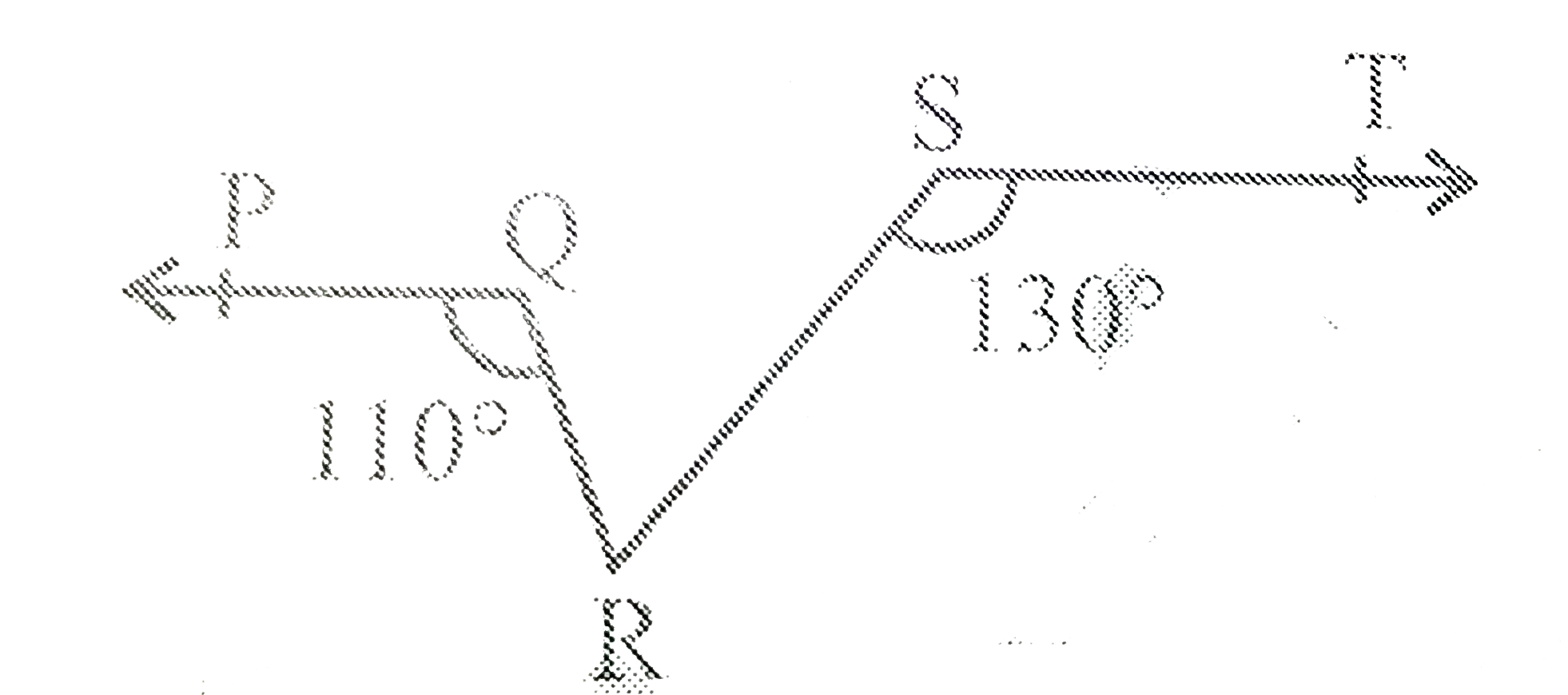 View Solution
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View Solution

