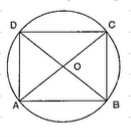
$A C a n d B D$ are chords of a circle that bisect each other. Prove that: $A C a n d B D$ are diameters $A B C D$ is a rectangle .

Video Solution

Text Solution

Verified by Experts

We conclude from the given information
$A B$ and $C D$ are the two chords of a circle
Lets assume the point of intersection be $O$ .
Construction
Join $A B, B C, C D$ and $A D$ .
In triangles $A O B$ and $C O D$ ,
$∠ A O B = ∠ C O D$ ...(Vertically opposite angles)
$O B = O D$ ....( $O$ is the mid-point of $B D$ )
$O A = O C$ ....( $O$ is the mid-point of $A C$ )
$△ A O B ≅ △ C O D$ .... $S A S$ test of congruence
$∴ A B = C D$ .... $c . s . c . t$ .
Similarly,
we can prove
$△ A O D ≅ △ B O C$ , then we get
$A D = B C$ .... $c . s . c . t .$
So, $□ A B C D$ is a parallelogram, since opposite sides are equal in length.
So, opposite angles are equal as well.
So, $∠ A = ∠ C$
Also,
for a cyclic quadrilateral opposite angles add up to $180^{\circ}$
So,
$∠ A + ∠ C = 180^{\circ}$
$∠ A + ∠ A = 180^{\circ}$
$∠ A = 90^{\circ}$
So,
$B D$ is the diameter.
Similarly, $A C$ is also the diameter.
(ii) Since $A C$ and $B D$ are diameters,
$∴ ∠ A = ∠ B = ∠ C = ∠ D = 90^{\circ}$ ...Angle inscribed in a semi circle is a right angle.
Hence, parallelogram $A B C D$ is a rectangle..

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a

Arectangle
Bsquare
Ctrapezium
Dparallelogram

RD SHARMA-CIRCLE -All Questions

Home
Ask Doubt
Profile