A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC
12 cm
20 cm
24 cm
30 cm
The correct Answer is:C
To find the perimeter of triangle ABC formed by the tangents from point A to the circle and the tangent BC at point R on the minor arc PQ, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O and radius 5 cm. Point A is located 13 cm from O. Tangents AP and AQ are drawn from point A to points P and Q on the circle. A tangent BC is drawn at point R, which lies on the minor arc PQ.
Step 2: Calculate the Length of Tangents AP and AQ
Using the Pythagorean theorem in triangle OAP:
- OA = 13 cm (distance from center O to point A)
- OP = 5 cm (radius of the circle)
According to the Pythagorean theorem:
OA2=AP2+OP2
Substituting the known values:
132=AP2+52
169=AP2+25
AP2=169−25
AP2=144
Taking the square root:
AP=√144=12 cm
Since AP = AQ (tangents from a point outside the circle are equal), we have:
AQ=12 cm
Step 3: Use the Properties of Tangents
Since BC is a tangent at point R, we can use the property of tangents from an external point:
- BR = BP (tangent from B to the circle)
- CR = CQ (tangent from C to the circle)
Step 4: Express the Perimeter of Triangle ABC
The perimeter of triangle ABC is given by:
Perimeter=AB+BC+CA
Since BC can be expressed as:
BC=BR+RC
We can substitute:
Perimeter=AB+(BR+RC)+CA
Using the properties of tangents:
- BR = BP
- RC = CQ
Thus:
Perimeter=AB+BP+CQ+CA
Step 5: Substitute Known Values
Since we know:
- AP = AQ = 12 cm
- AB = AP = 12 cm
- AC = AQ = 12 cm
We can substitute:
Perimeter=AB+BP+CQ+CA
Perimeter=AP+CQ+AP
Perimeter=12+12+12=24 cm
Conclusion
The perimeter of triangle ABC is:
Perimeter=24 cm
---
We have a circle with center O and radius 5 cm. Point A is located 13 cm from O. Tangents AP and AQ are drawn from point A to points P and Q on the circle. A tangent BC is drawn at point R, which lies on the minor arc PQ.
Using the Pythagorean theorem in triangle OAP:
- OA = 13 cm (distance from center O to point A)
- OP = 5 cm (radius of the circle)
OA2=AP2+OP2
Substituting the known values:
132=AP2+52
169=AP2+25
AP2=169−25
AP2=144
Taking the square root:
AP=√144=12 cm
AQ=12 cm
Since BC is a tangent at point R, we can use the property of tangents from an external point:
- BR = BP (tangent from B to the circle)
- CR = CQ (tangent from C to the circle)
The perimeter of triangle ABC is given by:
Perimeter=AB+BC+CA
BC=BR+RC
We can substitute:
Perimeter=AB+(BR+RC)+CA
- BR = BP
- RC = CQ
Perimeter=AB+BP+CQ+CA
Since we know:
- AP = AQ = 12 cm
- AB = AP = 12 cm
- AC = AQ = 12 cm
Perimeter=AB+BP+CQ+CA
Perimeter=AP+CQ+AP
Perimeter=12+12+12=24 cm
The perimeter of triangle ABC is:
Perimeter=24 cm
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4cm. Find the radius of the circle.
View SolutionFrom a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral PQOR is
View SolutionA line through the centre O of a circle of radius 7 cm cuts the tangent, at a point P on the circle, at Q such that PQ=24cm . Find OQ .
View SolutionTake a point O on the plane of the paper. With O as centre draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P .
View SolutionTake a point O on the plane of the papr. With O as centre draw a circle of radius 4 cm. Take point P on this circle and draw a tangent at P.
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
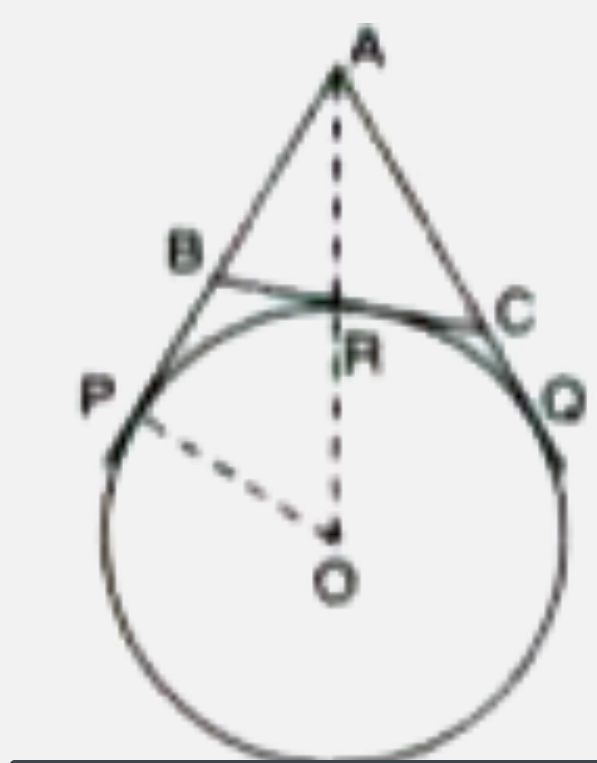 View Solution
View SolutionA point is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
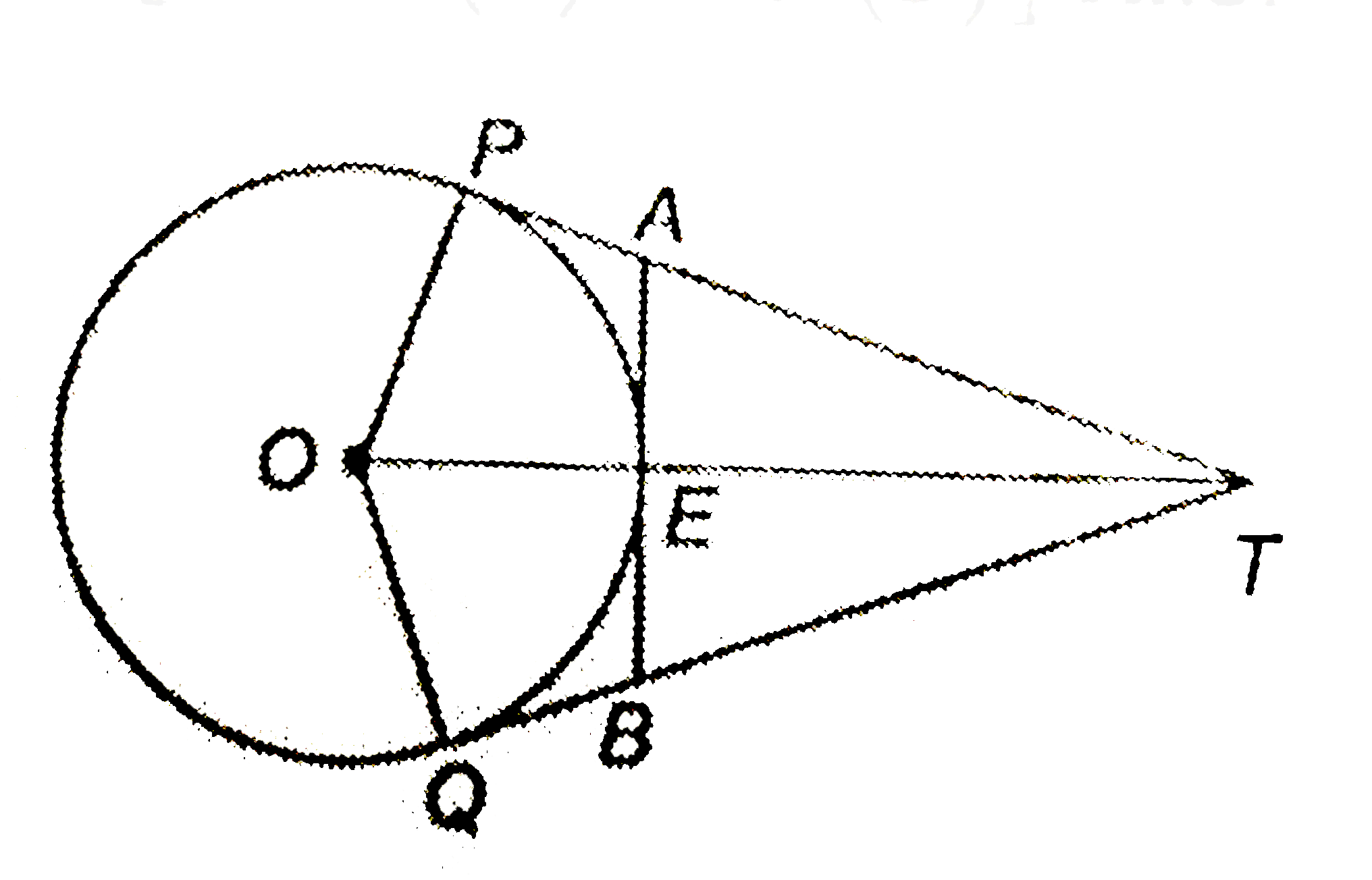 View Solution
View SolutionO is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB=15cm . Find OB .
View Solution

