A region in the x−y plane is bounded by the curve y=√25−x2 and the line y=0 . If the point (a,a+1) lies in the interior of the region, then (a)a∈(−4,3) (b) a∈(−∞,−1) ∪ (3,∞) (c)a∈(−1,3) (d) none of these
a∈(−4,3)
a∈(−∞,−1)∈(3,∞)
a∈(−1),3)
none of these
The correct Answer is:3
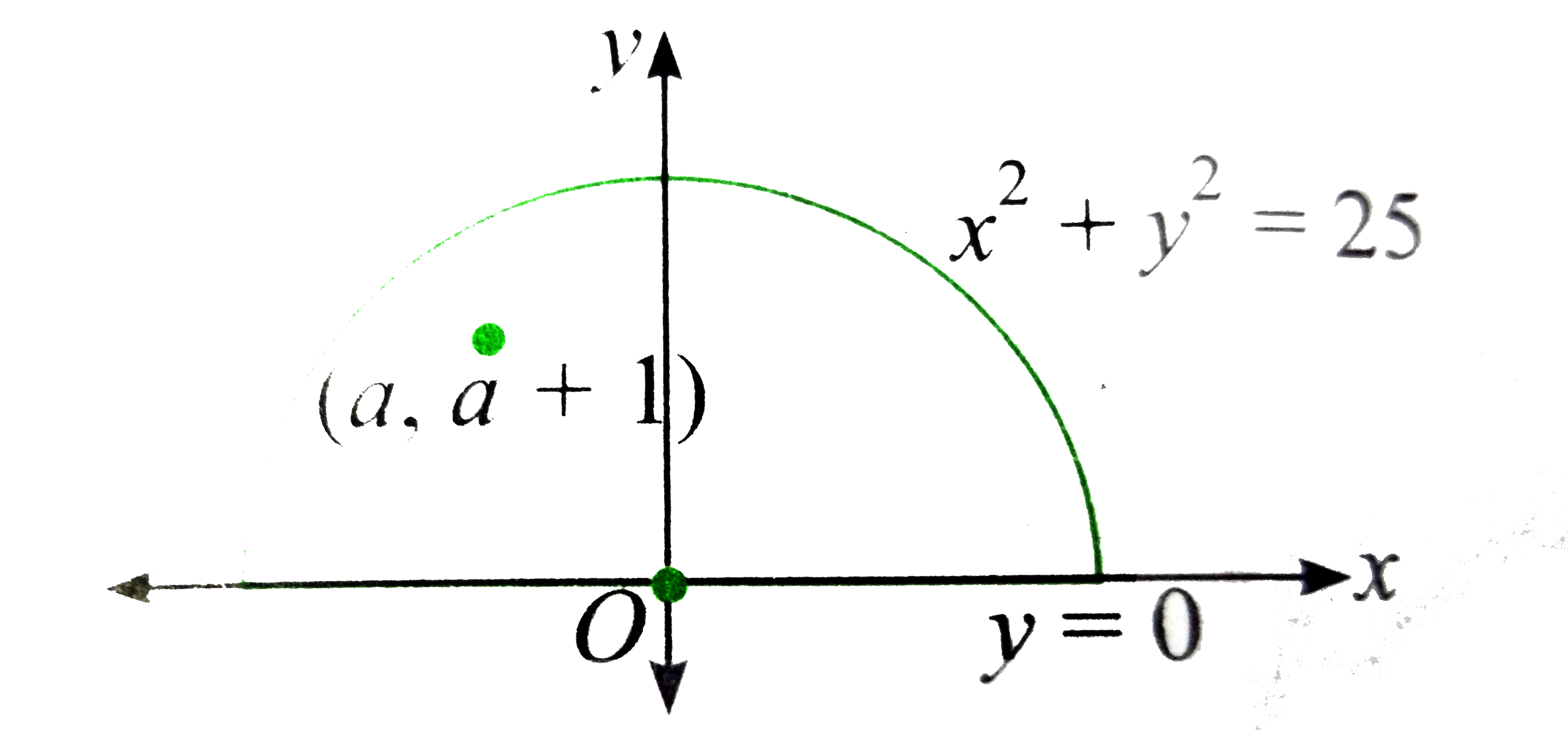
y=√25−x2 and y=0 bound the semicircle above the x-axis .
Therefore,
a+1>0 (1)
and a2+(a+1)2−25<0 or 2a2+2a−24<0
or a2+a−12<0
or −4<a<3 (2)
From (1) and (2),
−1<a<3
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the area of the region bounded by the curve y2=4xand the line x=3.
View SolutionFind the area of the region bounded by the curves y=x3 and the lines y=x+6 and y=0.
View SolutionThe area of the region bounded by the curve C:y=x+1x2+1 nad the line y=1 , is
View SolutionThe area of the region bounded by the curve y=x3 , and the lines , y=8 and x=0, is
View SolutionSketch the region bounded by the curves y=√5−x2 and y=|x−1| and find its area.
View SolutionThe area of the region bounded by the curve x=2y+3 and the lines y=1,y=−1 is
View SolutionFind the area of the region bounded by the curve y=x3 and the lines y = x + 6 and y =0.
View SolutionArea (in square units) of the region bounded by the curve y2=4x,y-axis and the line y=3 , is
View SolutionArea of the region bounded by the curve y=tanx and lines y = 0 and x = 1 is
View SolutionThe area of the region bounded by the curve y = x + 1 and the lines x=2,x=3, is
View Solution
