ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM=MA=12AB
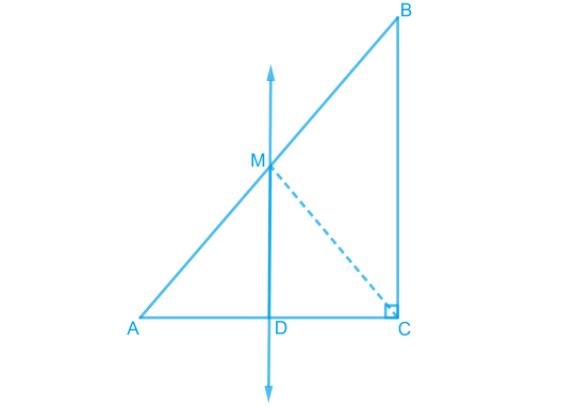
(i) In ΔABC,
It is given that M is the mid-point of AB and MD∣∣BC.
∴ D is the mid-point of AC. [Converse of mid-point theorem]
(ii) As DM∣∣CB and AC is a transversal,
∠MDC+∠DCB=180∘[Co-interior angles]
∠MDC+90∘=180∘
∠MDC=90∘
∴ MD⊥AC
(iii) Join MC
In ΔAMDand ΔCMD,
AD=CD (D is the mid-point of side AC)
∠ADM=∠CDM (Each 90∘)
DM=DM(Common)
∴ ΔAMD≅ΔCMD (By SAS congruence rule)
Therefore,AM=CM (By CPCT)
However, we also know that AM=12AB (M is the mid-point of AB)
∴ CM=AM=12AB
Similar Questions
ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
CP=12ABView SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔAPC≅ΔBPDView SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔDBC≅ΔACBView SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB
 View Solution
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
 View Solution
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.View Solution

