ABCD is a parallelogram. AB is produced to E so that BE=AB. Prove that ED bisects BC
"hereAB=BE (given)
AB=CD (opposite sides of a parallelogram)
therefore BE=CD....(1)
Let DE intersects BC at F
Now in △CDF and△BEF
∠DCF=∠EBF (since AB∥CD)
∠DFC=∠EFB (vertically opposite angles)
BE=CD (from (1))
from angle sum ∠CDF=∠BEF
from ASA theorem ,△CDF≅△BEF
from CPCT , BF=FC
Thus, ED bisect BC"
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD) - Question 2 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
ABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
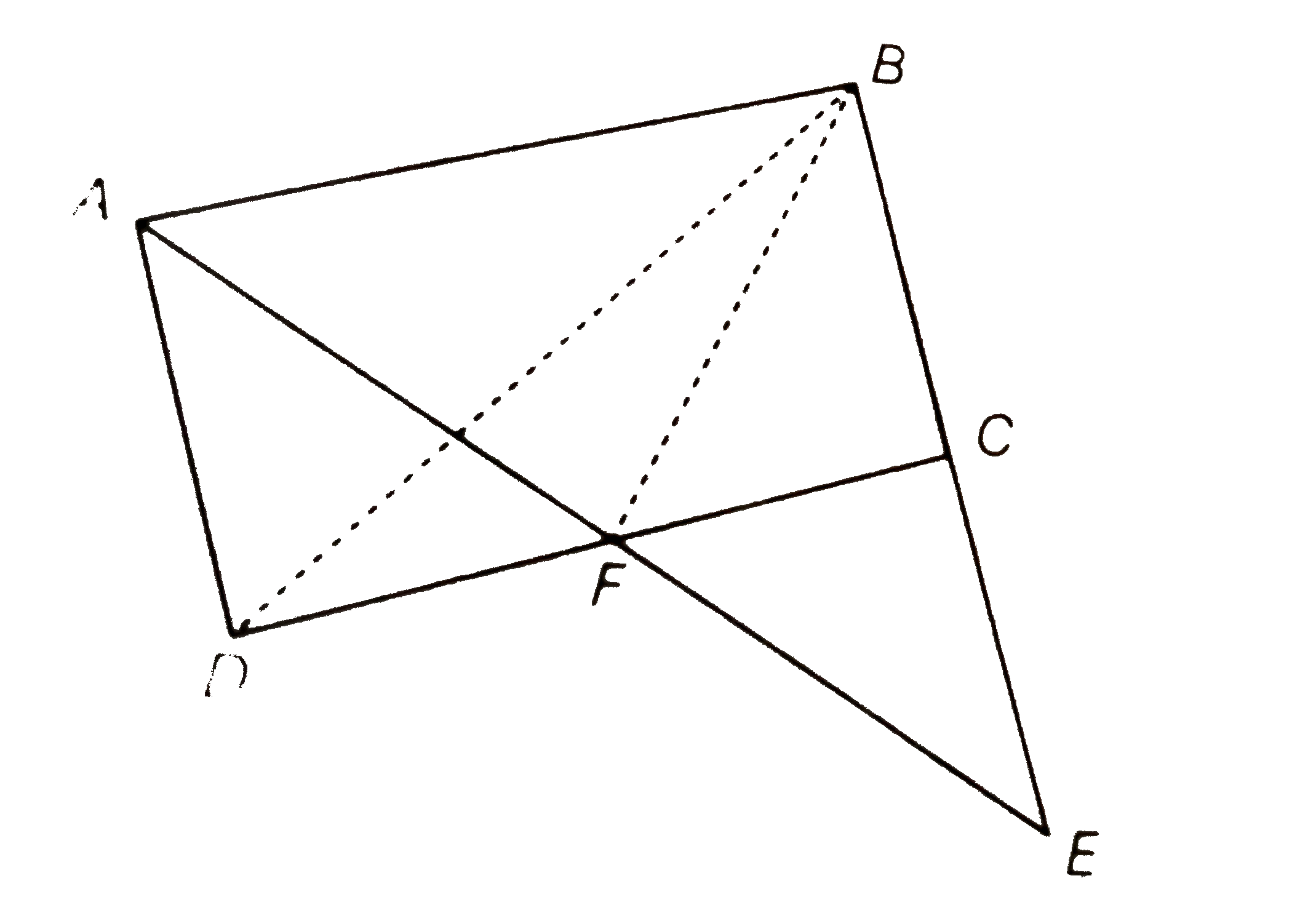
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.View SolutionABCD is a parallelogram. Side AB is produced on both sides to E & F as in figure such that BE = BC & AF = AD. Show that EC & FD when produced meets at right angle.
 View Solution
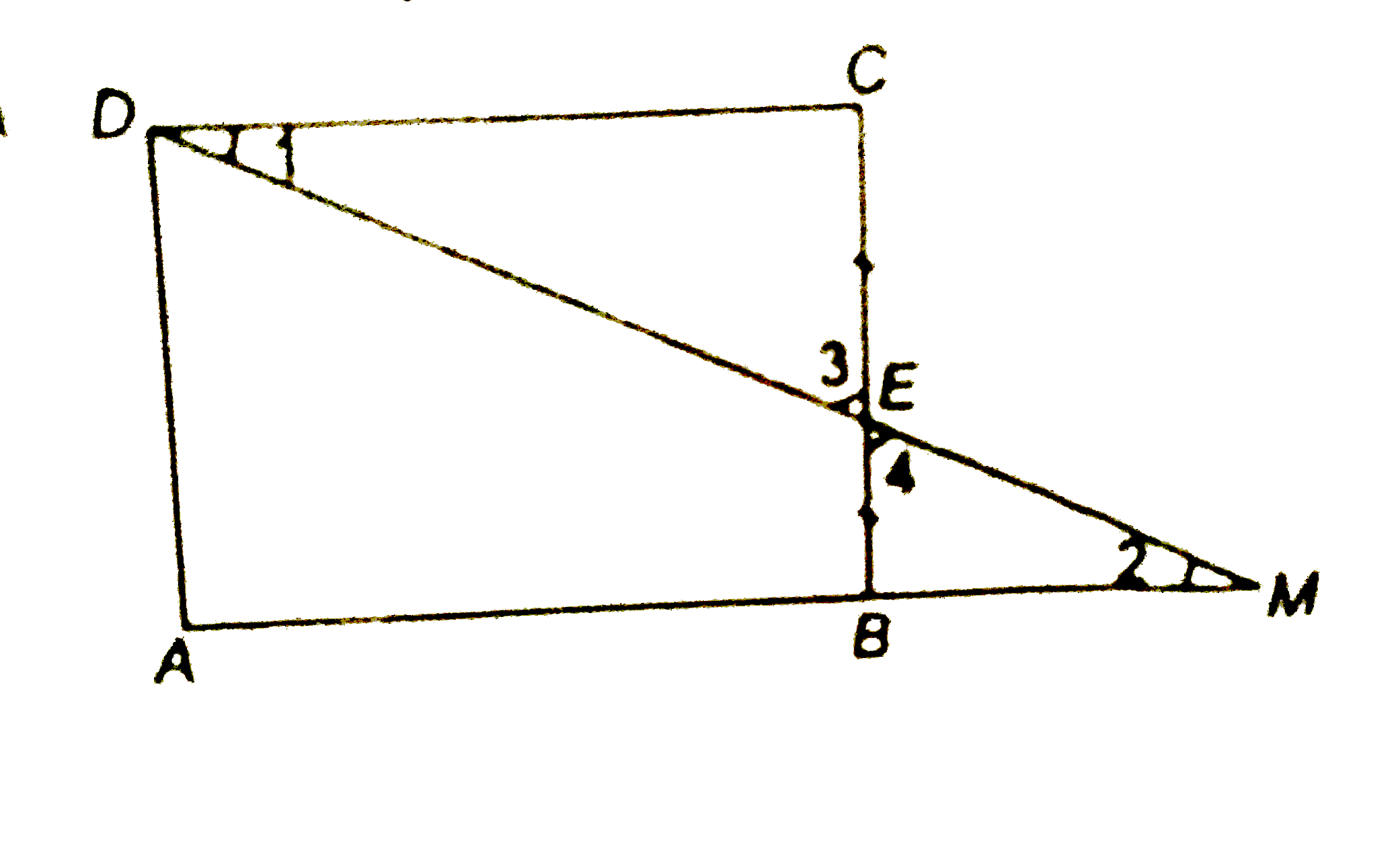
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
 View Solution
View SolutionABCD is a parallelogram. E is a point on extended side AB such that AB = BE. By joining D to E it intersects side BC at P. Find length of PC if BC = 15 cm.
View SolutionIn a △ABC, AD is the median drawn on the side BC is produced to E such that AD=ED. prove that ABEC is a parallelograms.
View Solution

