ABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
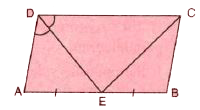
∠DEC=90∘
Step by step video & image solution for ABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that angleDEC= 90^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(A)
14 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B) (true/false)
10 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
ABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
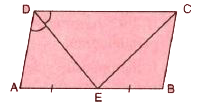
BC= BE
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
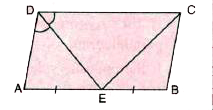
CE bisects angle C
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram, M is the mid-point of BD and BM bisects ∠B . Then, ∠AMB= 450 (b) 600 (c) 900 (d) 750
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH
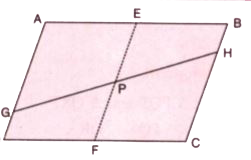
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that AE=EF=FC.
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
View Solution
