ABCD is a tetrahedron such that each of the , and has a right angle at A. If then is Solution in Punjabi
The correct Answer is:(c)
Step by step video & image solution for ABCD is a tetrahedron such that each of the triangleABC, triangleABD and triangleACD has a right angle at A. If ar(triangleABC) = k_(1). Ar(triangleABD)= k_(2), ar(triangleBCD)=k_(3) then ar(triangleACD) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (More Than One Correct Option Type Questions)
28 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Statement I And Ii Type Questions)
14 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise For Session 4
7 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
Given the equation of the line 3x−y+z+1=0and5x+y+3z=0. Then,which of the following is correct?
View Solutionlet →a=(ˆi+ˆj+ˆk) then find the unit vector along this vector
View SolutionFind the centre and radius of sphere 2(x−5)(x+1)+2(y+5)(y−1)+2(z−2)(z+2)=7.
View SolutionIn the quadratic equation ax2+bx+c=0. if δ=b2−4ac and α+β,α2+β2,α3+β3 are in G.P. and α,β are the roots of ax2+bx+c=0
View SolutionLet S={x∈(−π,π):x≠0,±π2}. The sum of all distinct solutions of the equation √2secx+cosecx+2(tanx−cotx)
=0 in the set S is equal to
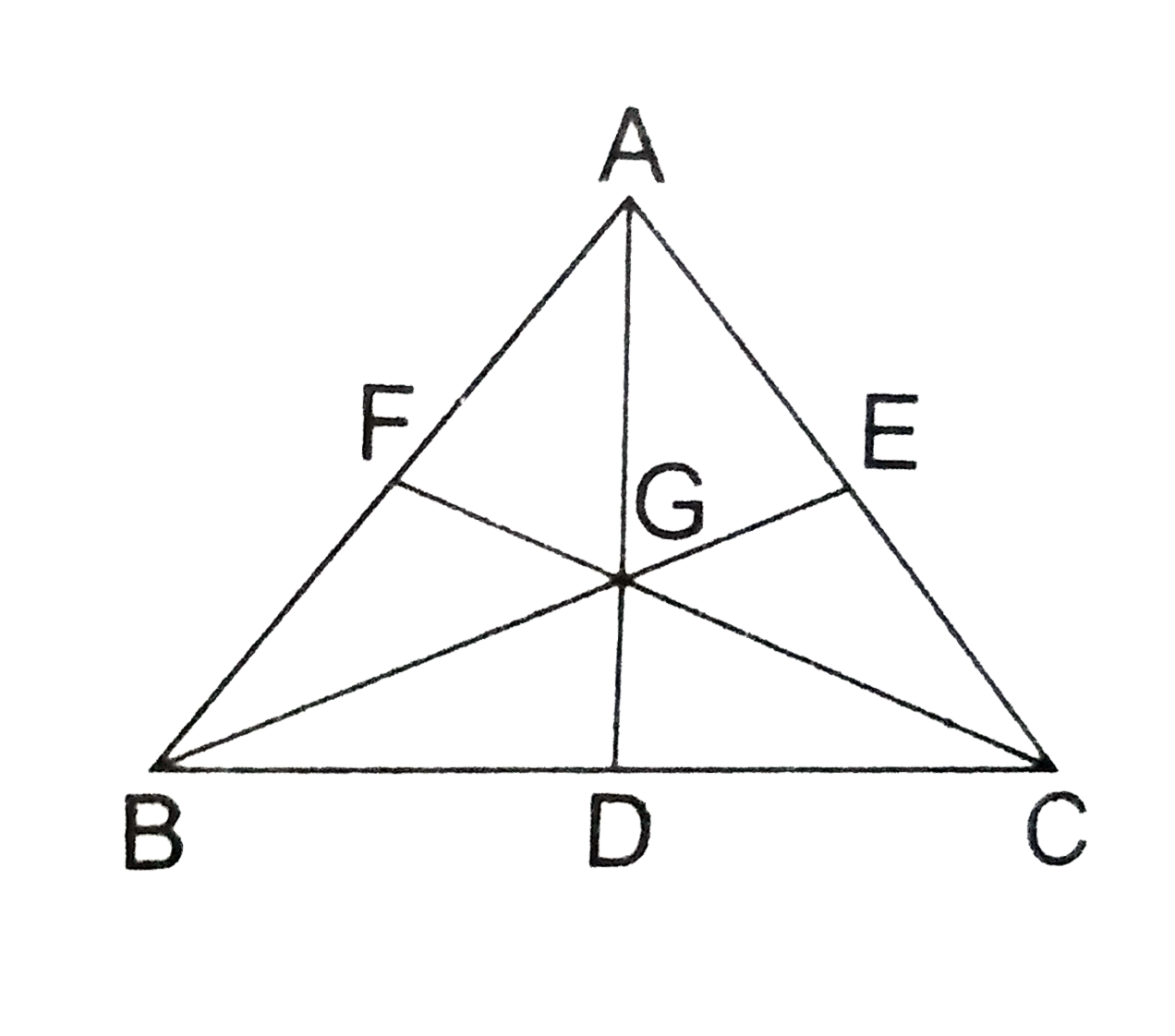
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
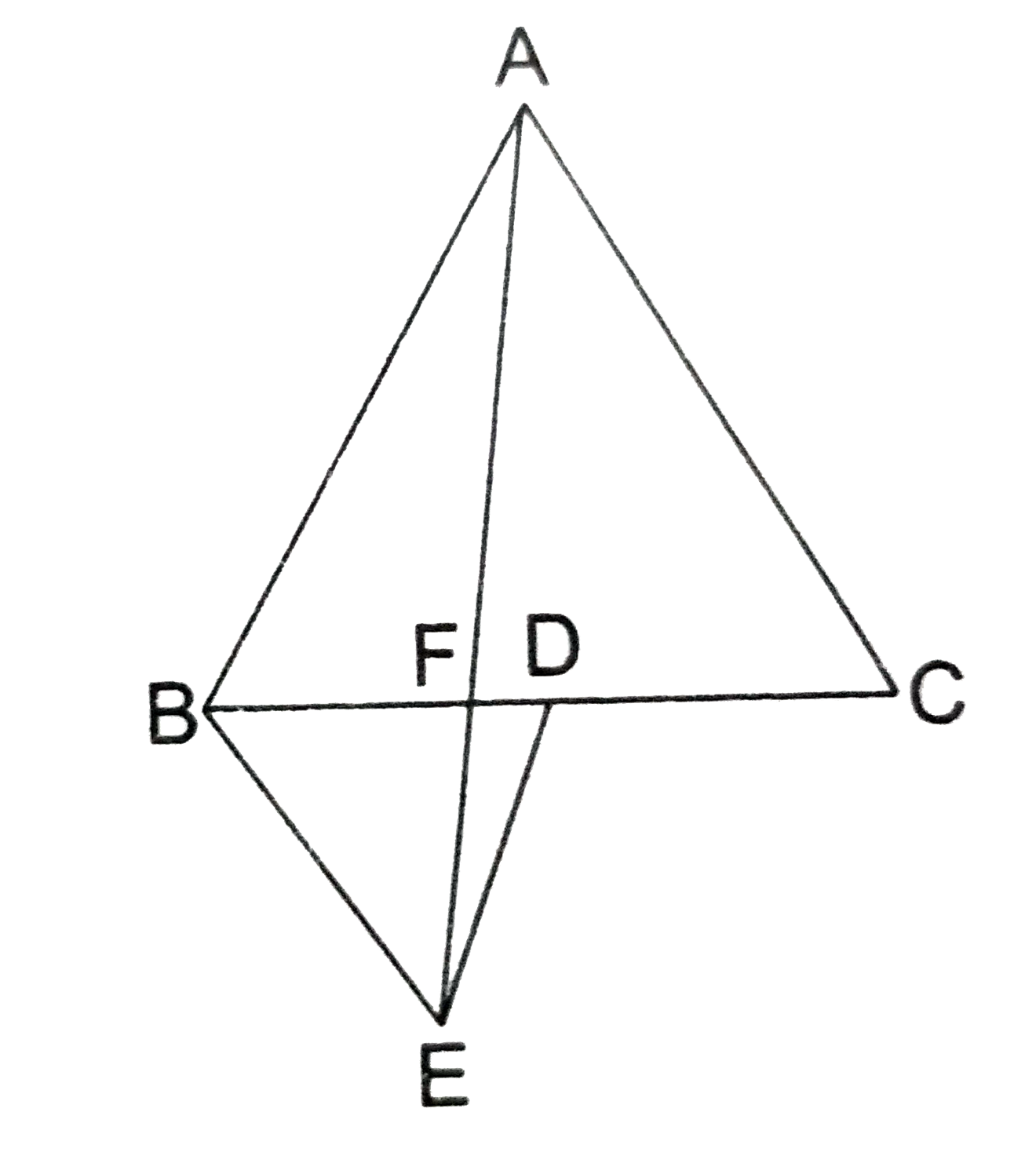
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
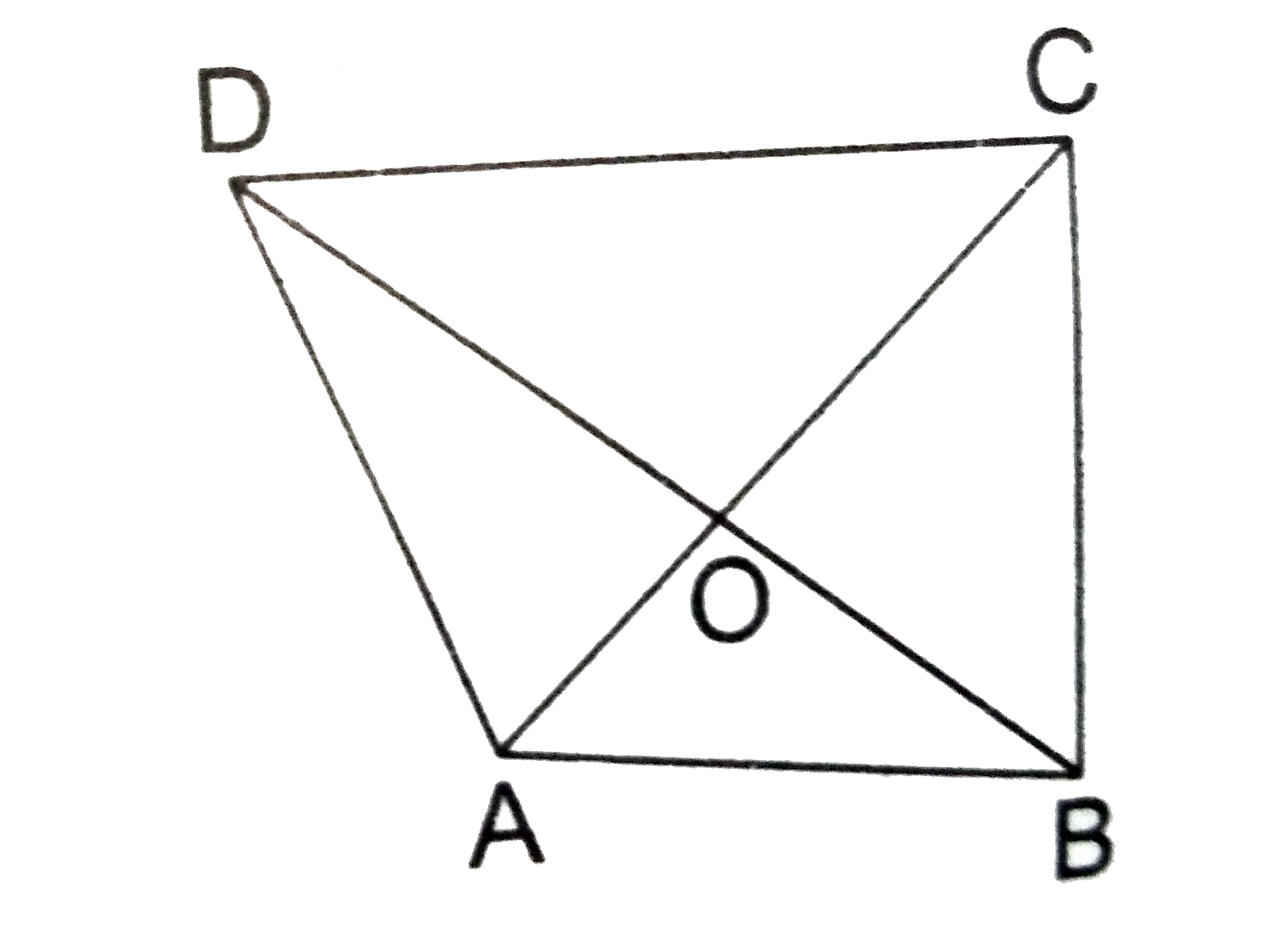
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionLet ABCD be a tetrahedron such that the edges AB, AC and AD are mutually perpendicular. Let the area of △ABC,△ACDand△ABD be 3, 4 and5 sq. units, respectively. Then, the area of the △BCD. Is
View SolutionIf ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionIf △ABC~△DEF,ar(△DEF)=100cm2andABDE=12, then ar(DABC) is
View SolutionIn △ABC, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=12ar(ABC)
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionLet ABCD be a tetrahedron such that the edges AB, AC and AD are mutually perpendicular. Let the area of triangleABC, triangleACD and triangleABD be 3, 4 and5 sq. units, respectively. Then, the area of the triangleBCD . Is
View Solution
