An equilateral triangle, if its altitude is 3.2cm
Text Solution
We know that , in an equilateral triangle all sides are equal and all angles are equal i.e., each angle is of 60∘ .
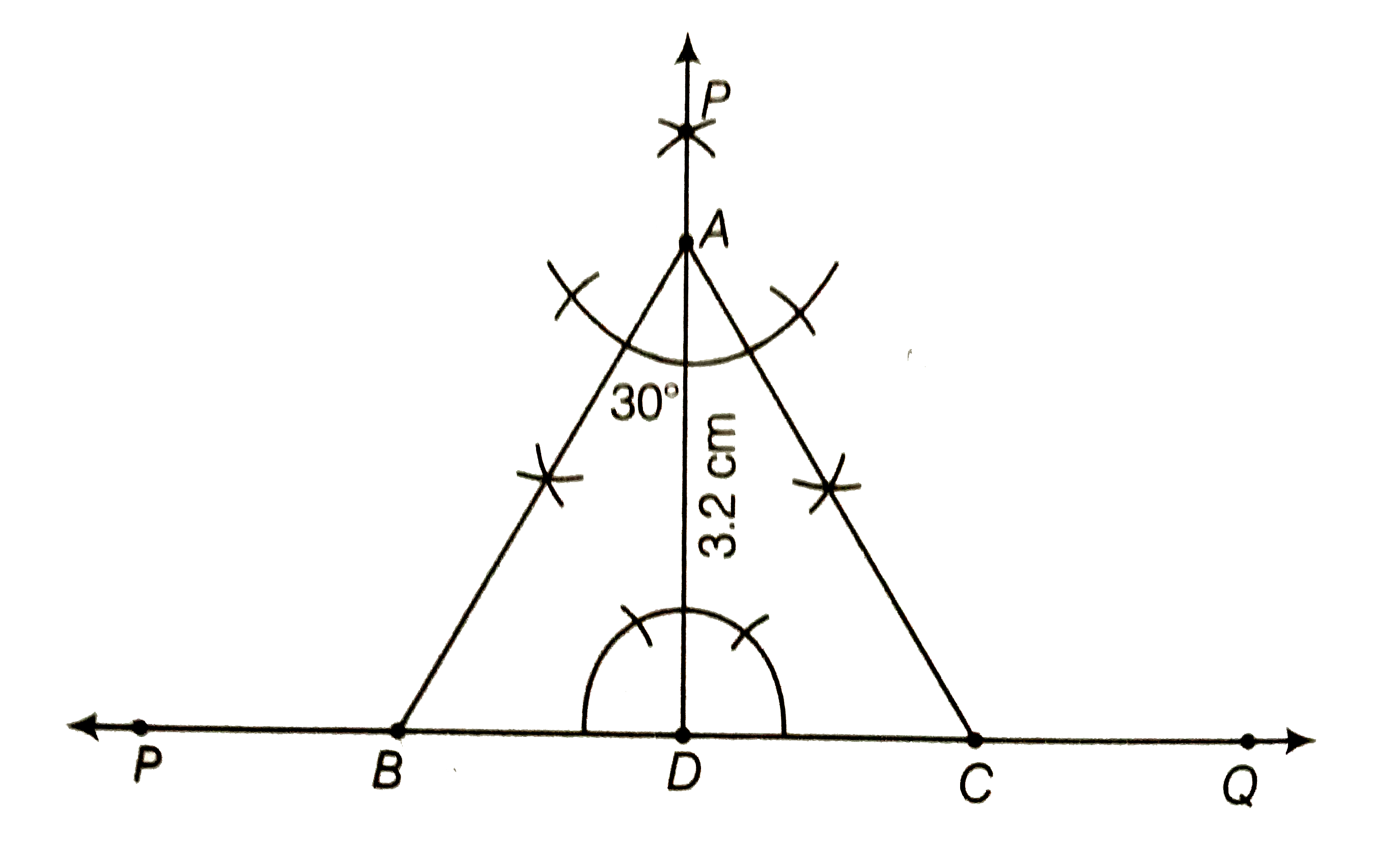
Given , altitudeof an equilateral triangle say ABC is 3.2cm . To construct the ΔABC use the following steps.
(i) Draw a line PQ.
(ii) Take a point D on PQ and draw a ray DE⊥PQ.
(iii) Cut the line segment AD of length 3.2cm from DE.
(iv) Make angles equal to 30∘ at A on both sides of AD say ∠CADand∠BAD , where B and C lie on PQ.
(v) Cut the line segment DC from PQ such that DC = AD
(vi) Join AC
Thus , ΔABC is the required triangle.
Justification
Here, ∠A=∠BAD+∠CAD
= 30∘+30∘=60∘
Also, AD⊥BC
∴∠ADB=90∘
In ΔABD∠BAD+∠DBA=180∘ [angle sum property]
30∘+90∘+∠DBA=180∘ [∠BAD=30∘, by construction]
∠DBA=60∘
Similary, ∠DCA=60∘
Thus , ∠A=∠B=∠C=60∘
Hence, ΔABC is an equilateral triangle.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the altitude of an equilateral triangle of side 8 cm.
A5√3B3√3C4√3D2√3Find the length of the altitude of an equilateral triangle of side 9√3cm.
A21 cmB15.5 cmC14 cmD13.5 cmIf each side of an equilateral triangle is 12 cm, then its altitude is equal to:
A6√2cmB3√2 cmC6√3cmD3√6 cm
Construct an equilateral triangle whose altitude is 4 cm.
View SolutionEach side of an equilateral triangle is 6 cm. Its altitude is
View SolutionFind the area of an equilateral triangle having altitude h cm.
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionFind the length of the altitude of an equilateral triangle of side 3√3cm
View Solution
