An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $3 \sqrt{3} c m$

Let $Δ A B C$ be an equilateral triangle of side 9cm. Let AD be one of its medians
Then, $A D ⊥ B C$ and $B D = 4.5 c m$ .
$∴ A D = \sqrt{A B^{2} - B D^{2}} = \sqrt{{(9)}^{2} - {(\frac{9}{2})}^{2}} c m = \frac{9 \sqrt{3}}{2} c m$
In and equilateral triangle, the centroid and circumcentre coincide and $A G : G D = 2 : 1$
$∴$ radius $= A G \frac{2}{3} A D (\frac{2}{3} \times \frac{9 \sqrt{3}}{2}) c m = 3 \sqrt{3} c m$

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

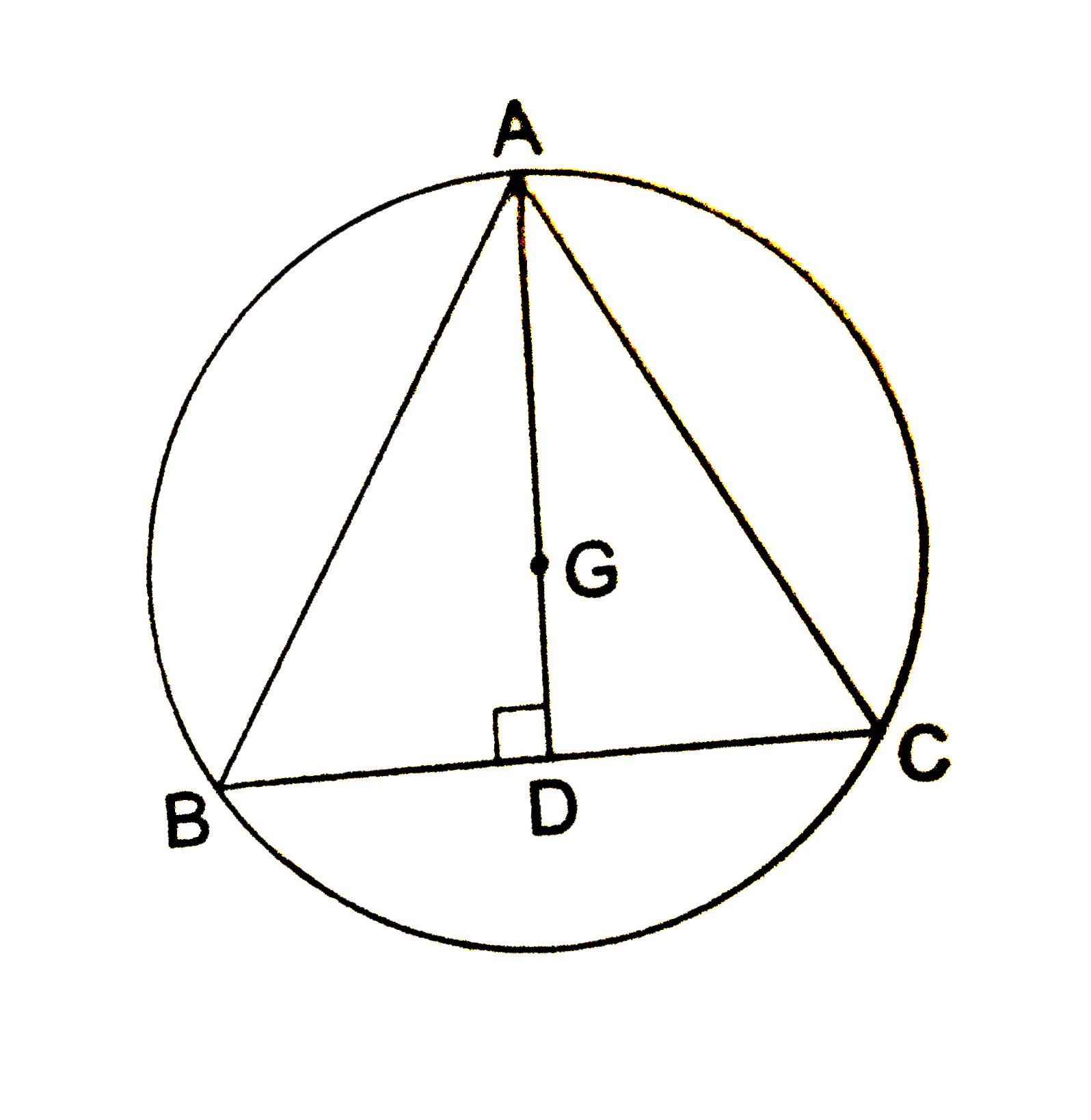
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circle is inscribed in a square. An equilateral triangle of side $4 \sqrt{3} c m$ is inscribed in that circle. The length of the diagonal of the square (in centimetres) is
A $4 \sqrt{2}$
B8
C $8 \sqrt{2}$
D16
Question 2 - Select One
An equilateral triangle is inscribed in a circle of radius $6$ cm. Find its side.
A $6 \sqrt{3}$
B $\frac{6}{\sqrt{3}}$
C $8 \sqrt{3}$
D $2 \sqrt{3}$
Question 3 - Select One
A circle is inscribed in an equilateral triangle and square is inscribed in that circle. The ratio of the areas of the triangle and the square is
A $\sqrt{3} : 4$
B $\sqrt{3} : 8$
C $3 \sqrt{3} : 2$
D $3 \sqrt{3} : 1$

RS AGGARWAL-CIRCLES -Exercise 12A

Home
Ask Doubt
Profile