AP and AQ are two tangents drawn from an external point A to a circle with centre O, P and Q are points of contact. If PR is a diameter, prove that OA∣∣RQ. Solution in Bengali
AP and AQ are two tangents to the circle with centre O and OP and OQ are two radii or the circle passing through poits of contact P and Q respectively.
∴OP⊥APandOQ⊥AQ
∴∠OPA=∠OQA=90∘
Now, ΔAOP≡ΔAOQ, [since ∠APO=∠AQO,OP=OQand hypotenuse OA is common to both.]
∴∠AOP=∠AOQ[∵ similar angles of congruent triangles] ......(1)

∴∠POQ=∠AOP+∠AOQ
=∠AOPQ+∠AOQ [from (1)]
=2∠AOQ......(2)
Again, ∠POQ is the central angle and ∠PRQ is the angle in circle produced by the arc PQ,
∴∠POQ=2∠PRQ [by theorem-34]
or,2∠AOQ=2∠PRQ[from (2)]
or,∠AOQ=∠PRQ=∠OQR[∵OQ=OR,∴∠ORQ=∠OQR]
∴∠AOQ=∠OQR.
But these are two alternate angles when OQ intersects the line segments OA and RQ, and they are also equal.
∴OA∣∣RQ. (Proved)
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
04:32View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
05:00View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
04:07View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
04:08View SolutionIn the given figure,two tangents PQ and PR are drawn to a circle with centre C from an external point P ,Prove that /_QPR=2/_OQR
04:24View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O.If /_PRQ=120^(@), then prove that OR=PR+RQ
01:37View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
03:51View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre 0. Prove that QORP is cyclic quadrileral.
09:20View SolutionIn the figure , PQ and PR are tangents drawn from and external point P to the circle with centre O. Q and R are the points of contact. If PQ = 5 cm then what is the length of segment PR ? Why ?
 04:55View Solution
04:55View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
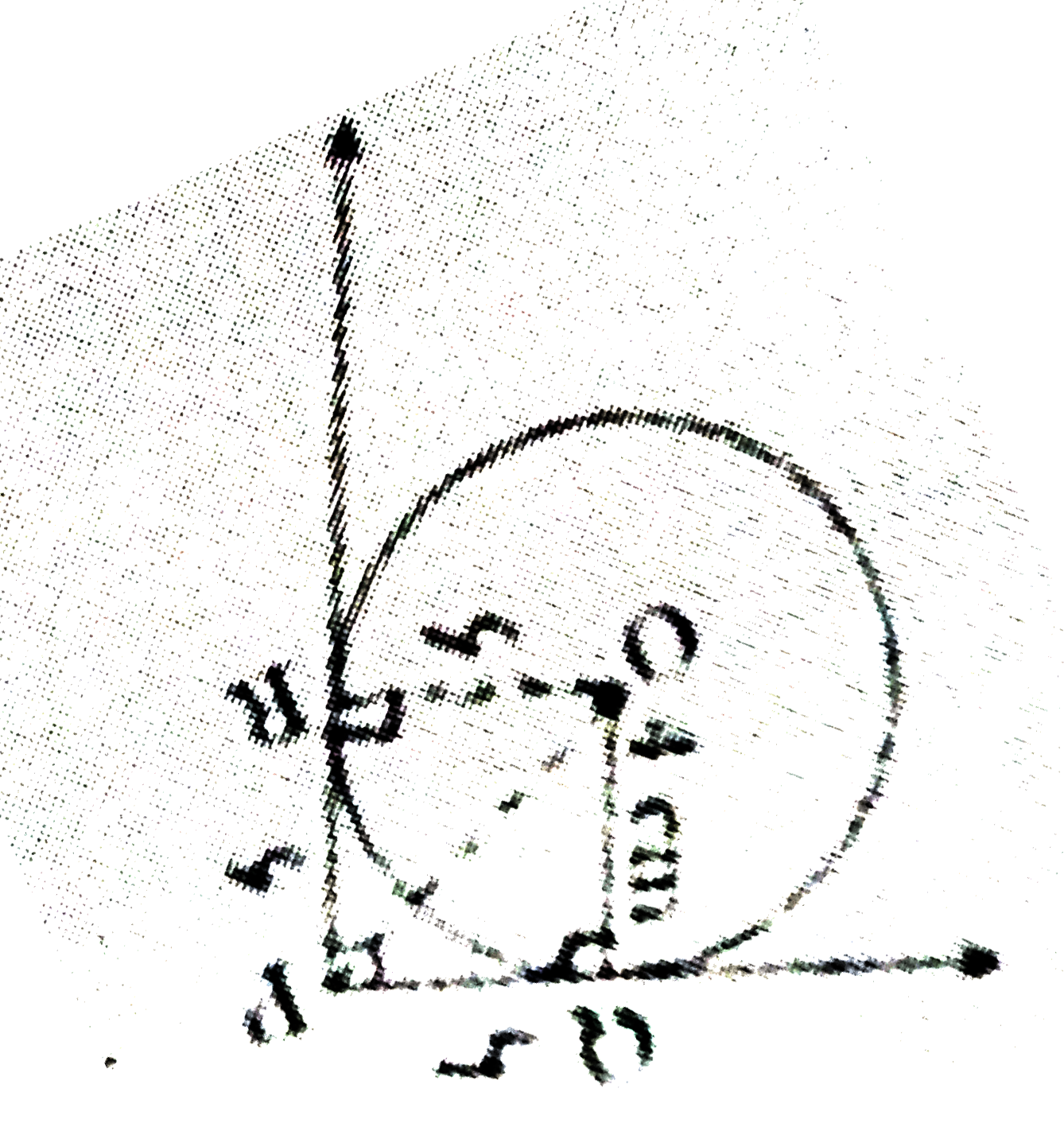 03:34View Solution
03:34View SolutionIn Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
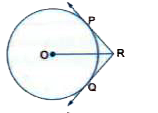 05:14View Solution
05:14View SolutionO Two tangents AP and AQ drawn from the outer point A of the central circle touch the circle P and Q points. If PR is a diameter, prove that, OA || RQ
06:04View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
04:01View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
03:14View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
 02:53View Solution
02:53View Solution

