As per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
The correct Answer is:SR=4
Step by step video & image solution for As per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.19videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.28videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.58videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘ - Question 2 - Select One
Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
APT = 2PQBPT<PQCPT>PQDPT=PQ - Question 3 - Select One
Two circles Intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
APT=2PQBPT<PQCPT>PQDPT=PQ
In the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
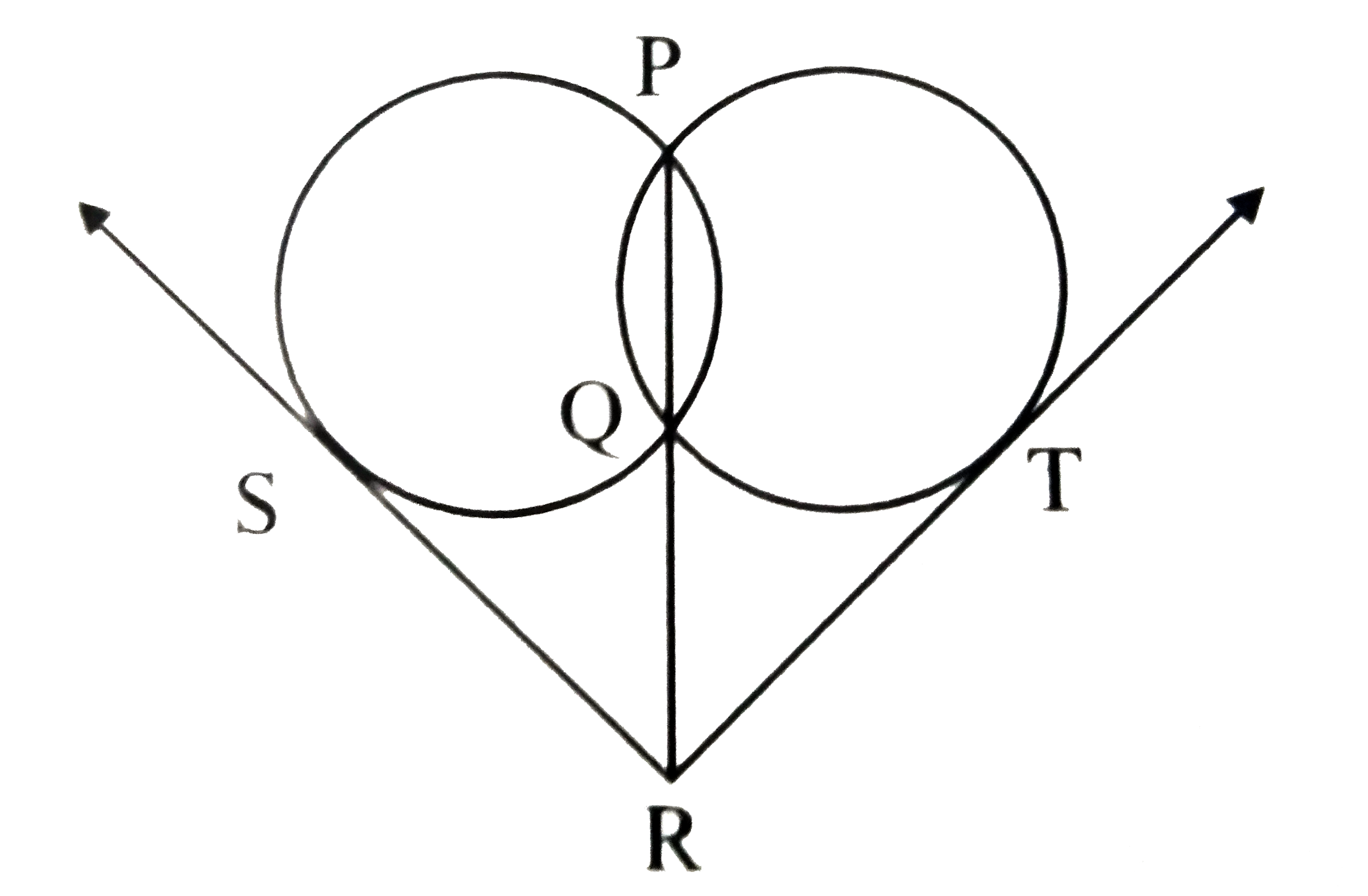 View Solution
View SolutionIn the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
View SolutionProve that two different circles cannot intersect each other at more than two points.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
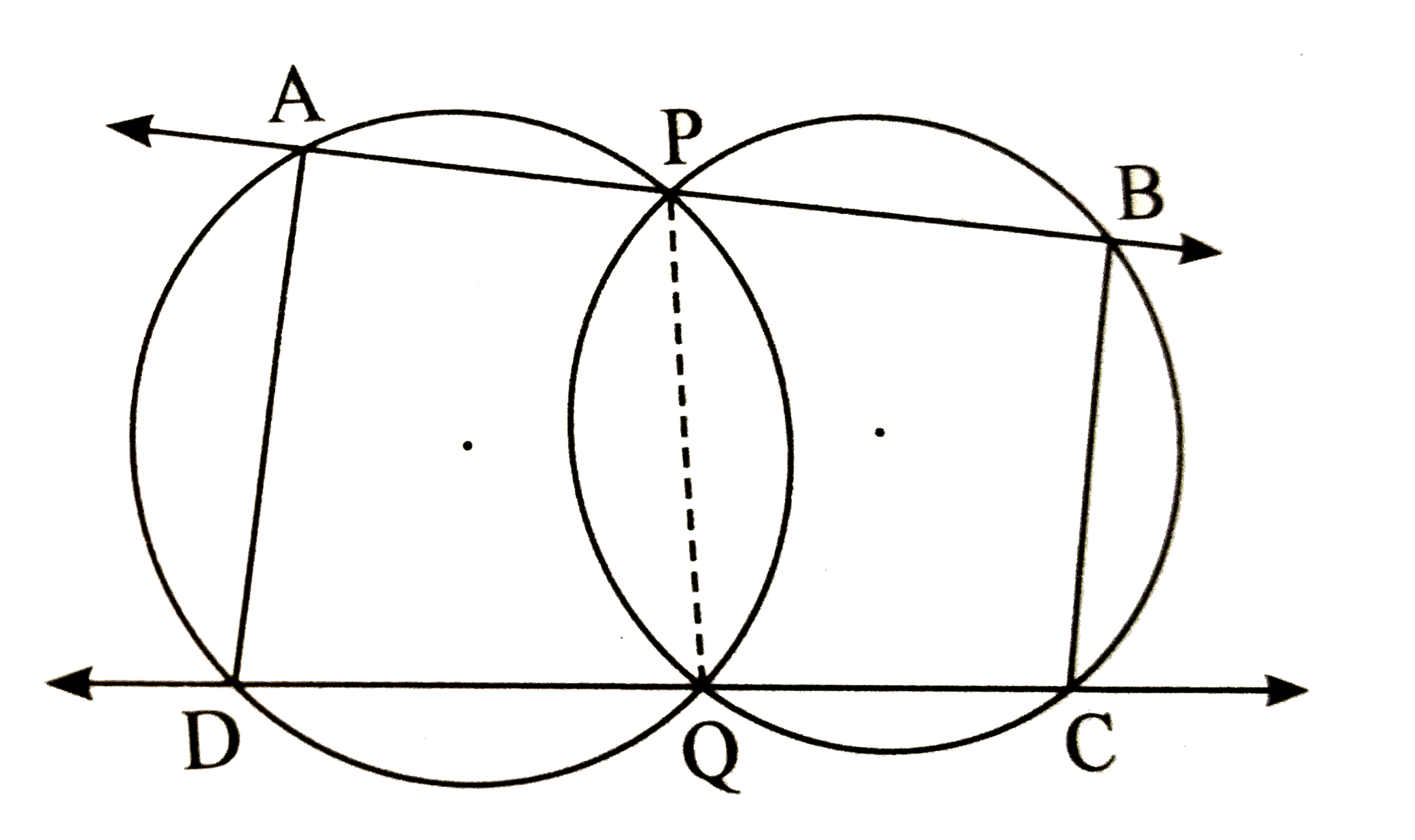 View Solution
View SolutionTwo circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
View Solution


