Chords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
The correct Answer is:chord cd
To prove that chord AB is equal to chord CD given that OE bisects angle AED, we can follow these steps:
1. Draw the Circle and Chords:
- Draw a circle with center O.
- Draw two chords AB and CD that intersect at point E.
2. Draw Perpendiculars from O:
- Draw a perpendicular OM from O to chord AB, and a perpendicular ON from O to chord CD.
3. Identify Triangles:
- We will analyze triangles OEM and OEN.
4. Angles in Triangles:
- Since OM and ON are perpendicular to the chords, we have:
- ∠OME = 90°
- ∠ONE = 90°
- Therefore, ∠OME = ∠ONE.
5. Angle Bisector:
- Since OE bisects angle AED, we have:
- ∠AEO = ∠DEO (by the definition of angle bisector).
6. Congruent Angles:
- Thus, we can say:
- ∠OEM = ∠OEN (since both are equal to ∠AEO and ∠DEO respectively).
7. Common Side:
- The side OE is common to both triangles, so:
- OE = OE.
8. Triangle Congruence:
- By the Angle-Angle-Side (AAS) criterion, triangles OEM and OEN are congruent:
- ΔOEM ≅ ΔOEN.
9. Corresponding Parts of Congruent Triangles:
- From the congruence of triangles, we have:
- OM = ON (corresponding parts of congruent triangles).
10. Equidistance of Chords:
- Since OM and ON are the perpendicular distances from the center O to the chords AB and CD respectively, and OM = ON, we conclude that the chords AB and CD are equidistant from the center O.
11. Conclusion:
- If two chords are equidistant from the center of the circle, then they are equal in length. Therefore, we conclude:
- Chord AB = Chord CD.
- Draw a circle with center O.
- Draw two chords AB and CD that intersect at point E.
- Draw a perpendicular OM from O to chord AB, and a perpendicular ON from O to chord CD.
- We will analyze triangles OEM and OEN.
- Since OM and ON are perpendicular to the chords, we have:
- ∠OME = 90°
- ∠ONE = 90°
- Therefore, ∠OME = ∠ONE.
- Since OE bisects angle AED, we have:
- ∠AEO = ∠DEO (by the definition of angle bisector).
- Thus, we can say:
- ∠OEM = ∠OEN (since both are equal to ∠AEO and ∠DEO respectively).
- The side OE is common to both triangles, so:
- OE = OE.
- By the Angle-Angle-Side (AAS) criterion, triangles OEM and OEN are congruent:
- ΔOEM ≅ ΔOEN.
- From the congruence of triangles, we have:
- OM = ON (corresponding parts of congruent triangles).
- Since OM and ON are the perpendicular distances from the center O to the chords AB and CD respectively, and OM = ON, we conclude that the chords AB and CD are equidistant from the center O.
- If two chords are equidistant from the center of the circle, then they are equal in length. Therefore, we conclude:
- Chord AB = Chord CD.
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(A)
14 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
Two equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
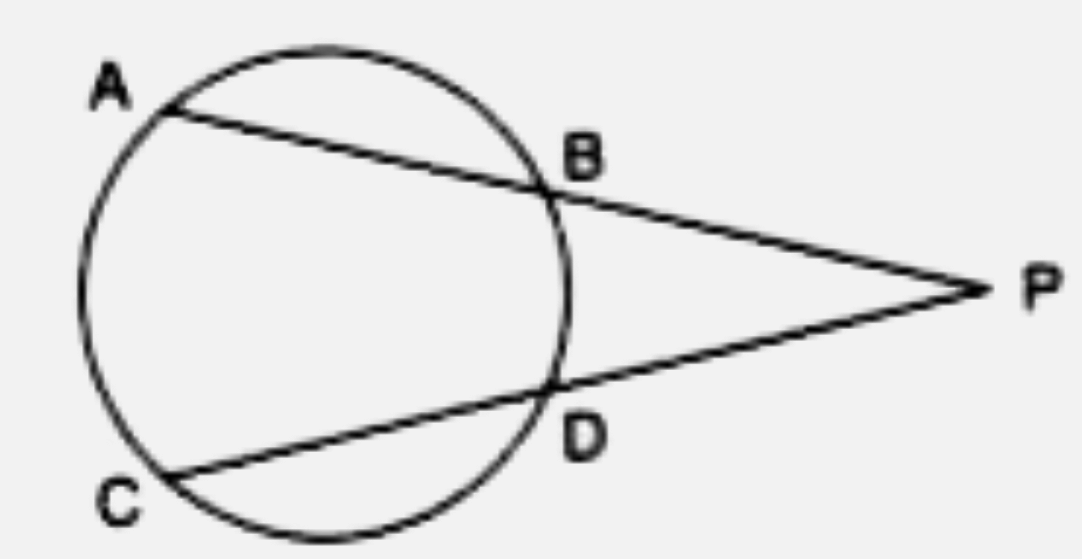
PA=PC.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PB=PD
View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
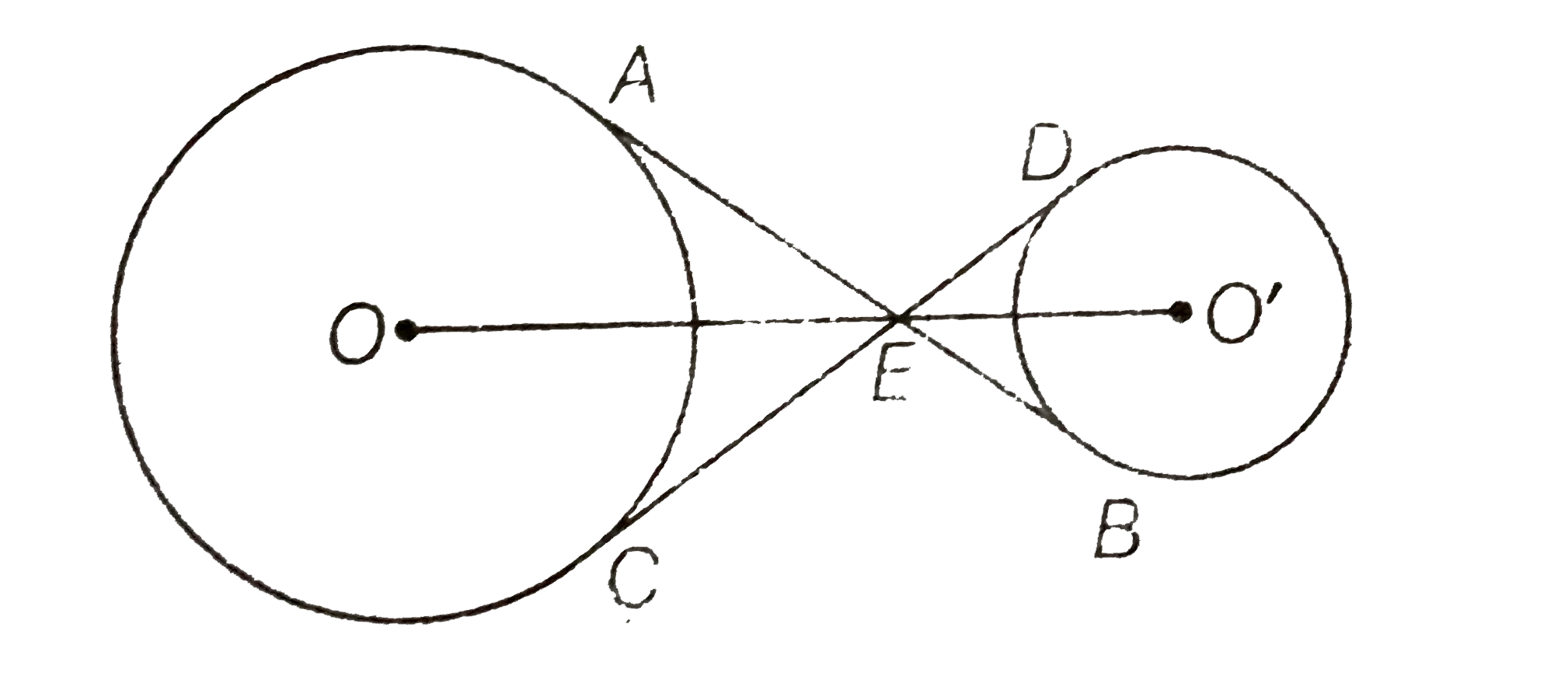
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View Solution
