Draw the graph of y=cos(|x|+π2)sinx. Is the function periodic ?
Video Solution
Text Solution
We have y=f(x)=cos(|x|+π2)sinx
Clearly, the domain of the function is R−{nπ,n∈Z}
f(x)=−sin|x|sinx
=⎧⎪⎨⎪⎩−sin(−x)sinx, x<0−sin(x)sinx, x>0
={1, x<0−1, x>0
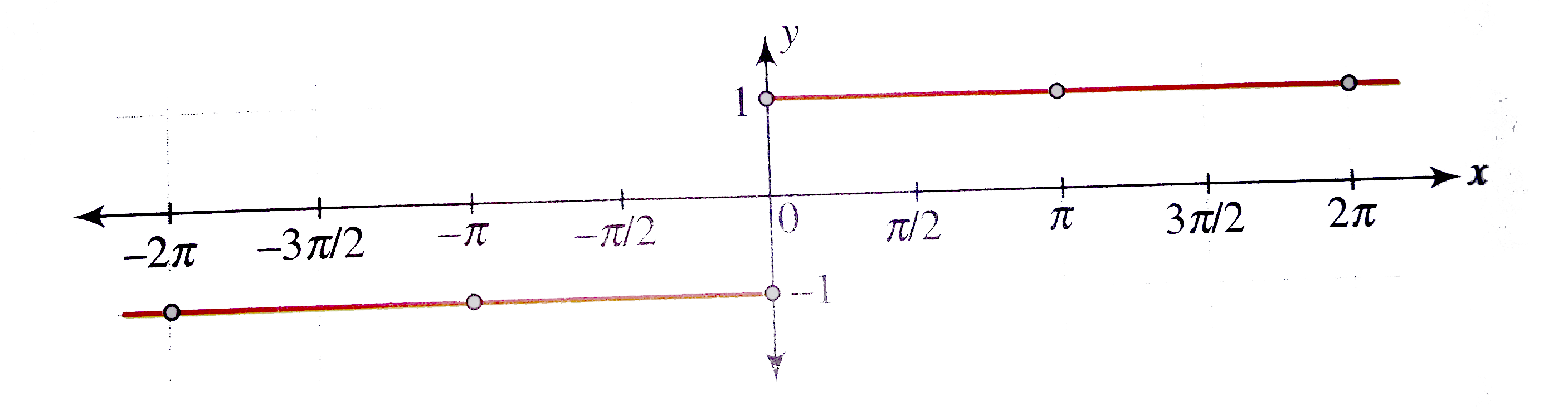
Clearly, from the graph, the function is not periodic.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y=cos2x.
View SolutionDraw the graph of y=sin3x.
View SolutionDraw the graph of y = x sin x.
View SolutionDraw the graph of y=cos(x−π4).
View SolutionDraw the graph of y=sin−1|x|.
View SolutionDraw the graph of y=sin2x.
View SolutionDraw the graph of y=sinxx.
View SolutionDraw the graph of y=3sin2x.
View SolutionDraw the graph of y=sin2x−cosx
View SolutionDraw graph of y = sin x
View Solution
