E and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
Given ABCD is a parallelogram and AE = CF
Construction Join BD, meet AC at point O.
Proof Since, diagonals of a parallelogram bisect each other.
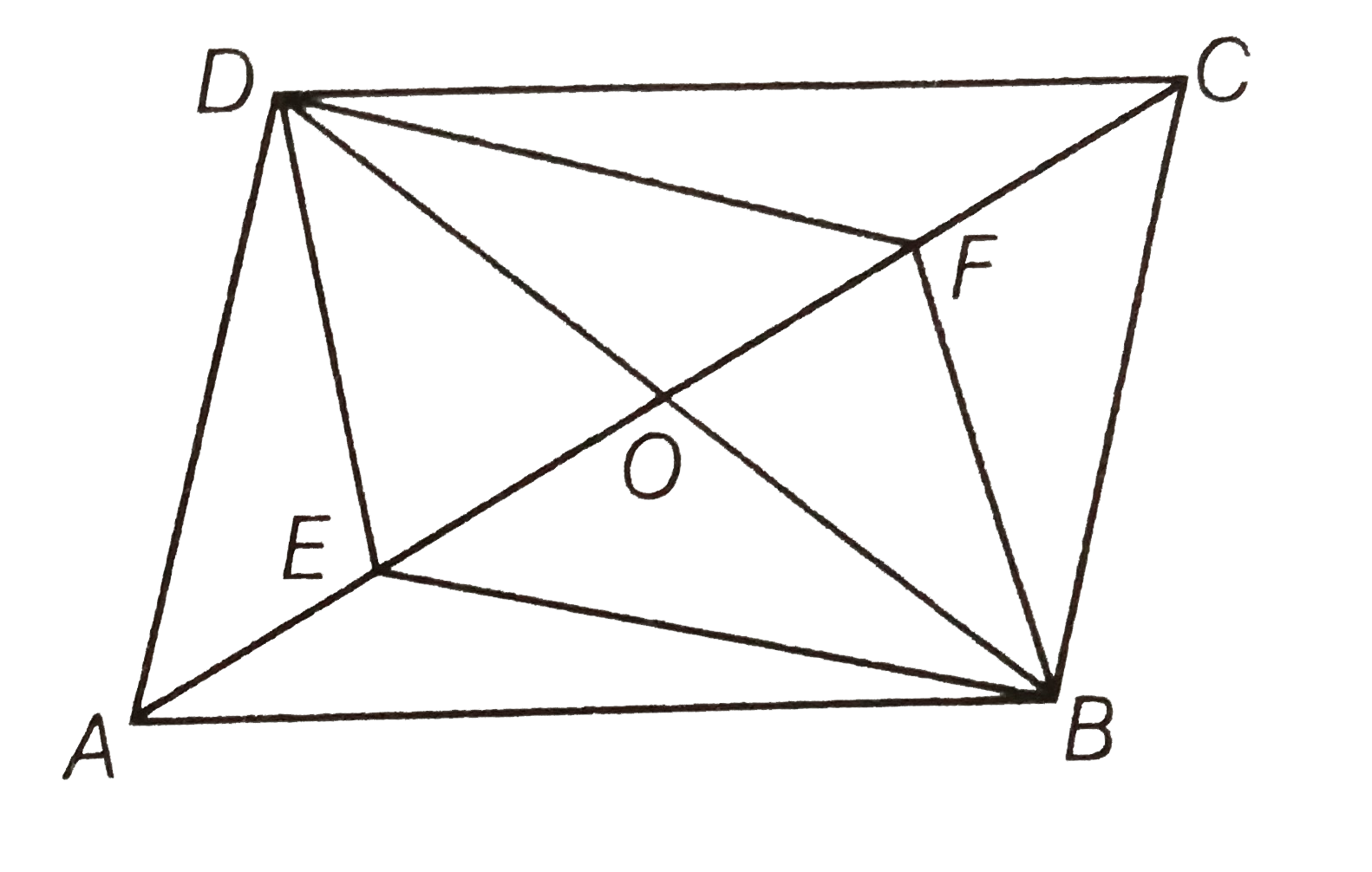
∴ OA=OC
and OD = OB
Now, OA=OC
and AE = CF [given]
⇒ OA−AE=OC−CF
⇒ OE=OF
Thus, BFDE is a quadrilateral whose diagonals bisect each other.
Hence, BFDE is a parallelogram. Hence proved.
Topper's Solved these Questions
Similar Questions
Two points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionPoint E and F lie on diagonals AC of a parallelogram ABCD such that AnE=CF. What type of quadrilateral is BFDE? From the given figure we see that BFDEis also a parallelogram.
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionIf the diagonals of a parallelogram are equal, then it is a
View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionABCD and APCR are the two parallelograms and AC is the common diagonal. Prove that PBRD is a parallelogram.
View SolutionIn the given figure, □ABCD is a parallelogram. If DM ⊥ AC and BN ⊥ AC, then show that □BNDM is a parallelogram.

View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View Solution
