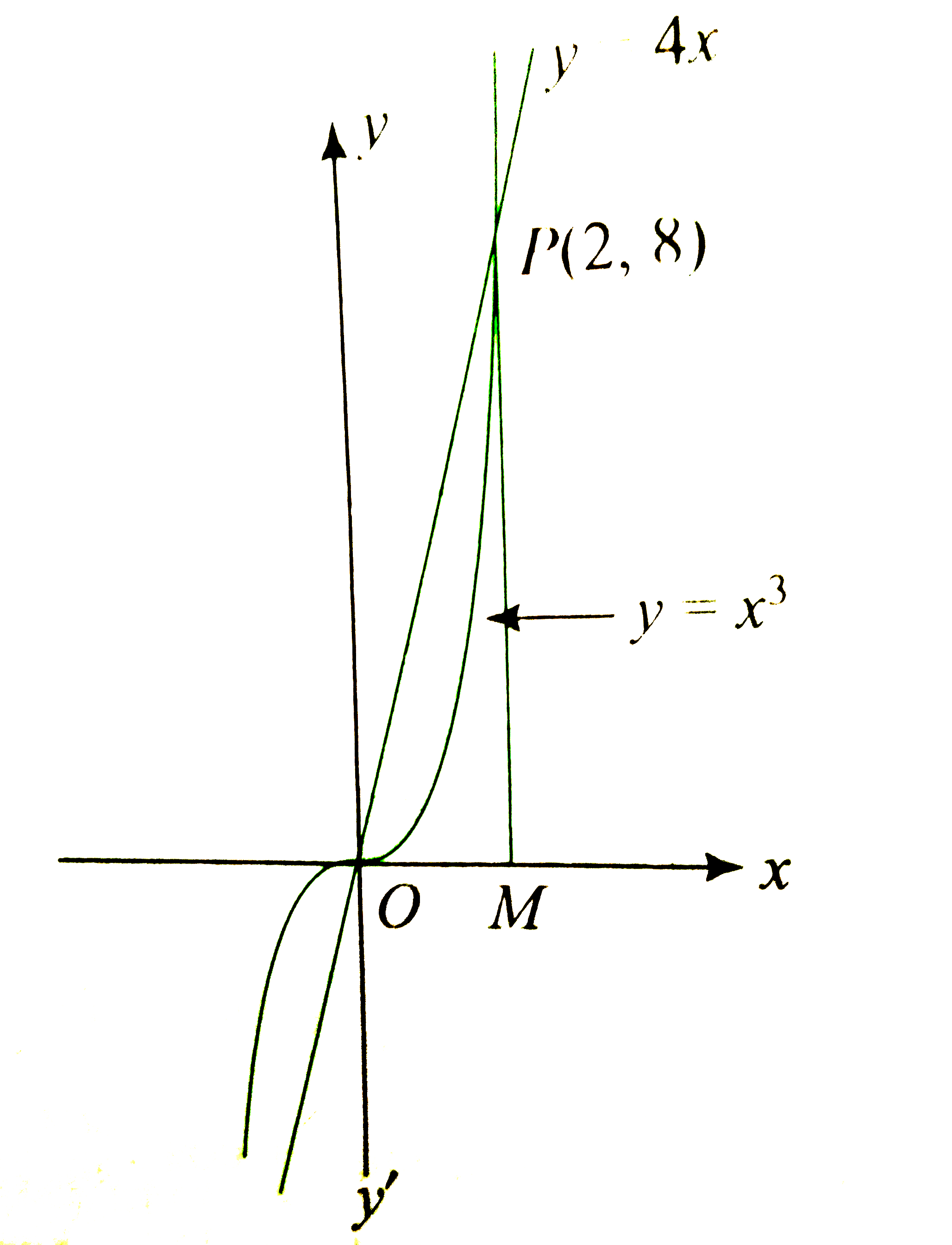
Find the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
The correct Answer is:4 sq. units
The line y=4x meets y=x3 at 4x=x3.
∴ x=0,2,−2⇒y=0,8,−8
⇒ A=∫20(4x−x3)=(2x2−x44)20=4 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type
40 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Find the area of the figure lying in the first quadrant and bounded by the curves y2=4x,x2=4y.
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0 and x=2 is:
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4and the lines x=0andx=2is(A) π (B) π2 (C) π3 (D) π4
View SolutionFind the area bounded by the curve y=2x−x2, and the line y=x
View SolutionFind the area bounded by the curves y=2x−x2 and the straight line y=−x.
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
View SolutionFind the area bounded by the curves y=4−x2 and the lines y=0andy=3
View SolutionFind the area of the region bounded by the curve y=x2 and the line y = 4 .
View SolutionFind the area of the region bounded by the curves y=x3 and the lines y=x+6 and y=0.
View SolutionThe area bounded by the curve x2=4ay and the line y=2a is
View Solution
