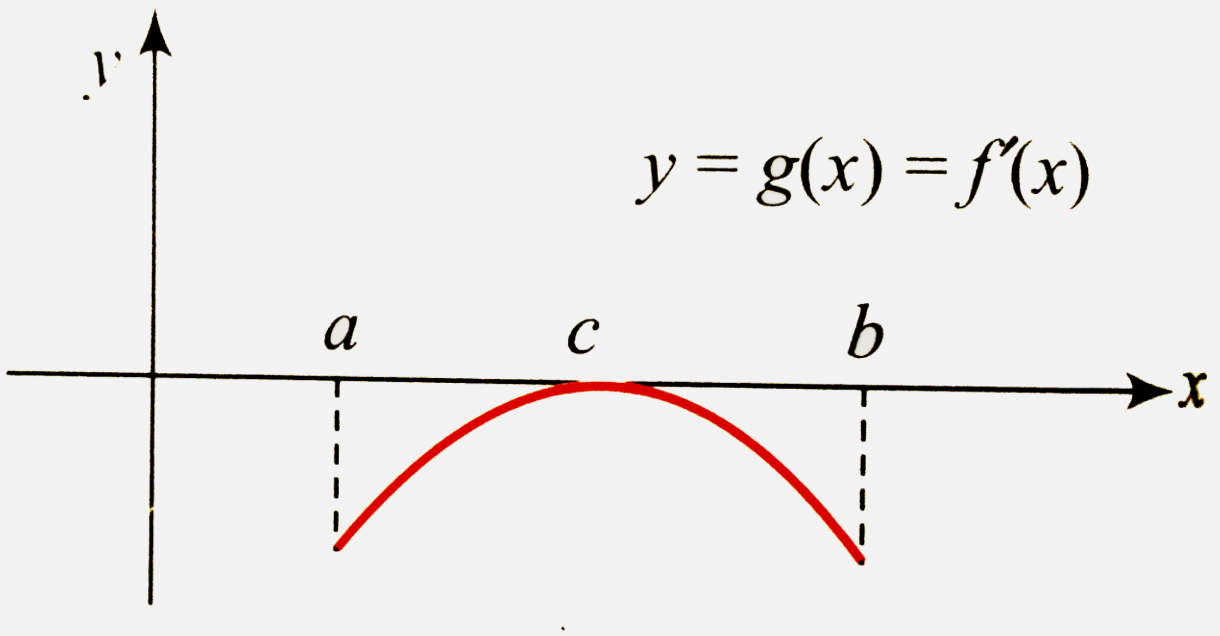
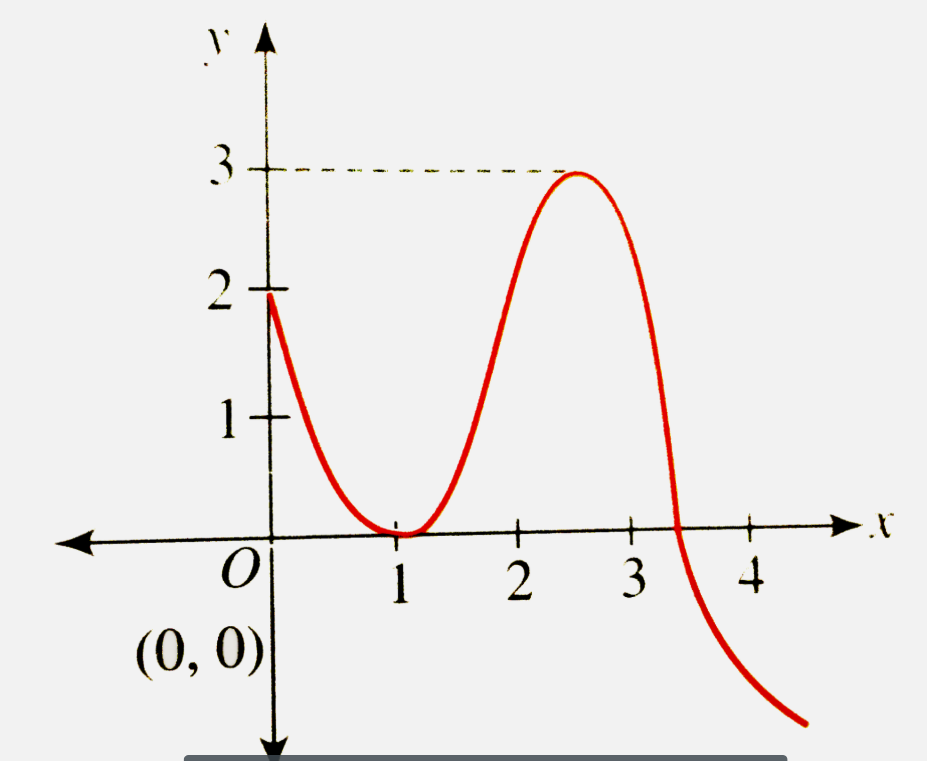
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
,(d) Find the points of local maxima/minima of y=f(x),a≤x≤b,
,
(e) f"(x)=0 has how many roots?
 Solution in Bengali
Solution in Bengali
(a) f'(x)≤0,∀x∈[a,b], so f(x) is a decreasing function and f(c)=0⇒f(x) is a decreasing function and x(c)=0⇒f(x) cuts x - axis once when x = c.
(b) We note that f(c) = 0, f'(c) = 0. Also tangent to f'(x) at x = c is y = 0. So f''(c) = 0 Therefore, x = c is repeated root of third order. So the equation f(x) = 0 has at least three repeated roots.
(c) We have f''(c) = 0 . So the graph of y = f (x) has one point of inflection at x = c.
(d) As f (x) is a decreasing function for all x∈(a,b),f(x) has no local maxima or minima.
(e) f''(c)=0⇒c is a root of f''(x) = 0.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.27
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.28
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.25
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
Find the asymptote of the function y=2x2+3x+1x if any.
View SolutionFind the horizontal, vertical and oblique asymptotes of each of the curves.
(a)y=xx+4(b)y=x2+4x2−1(c)y=x3x2+3x−10(d)y=x3+1x3+x(e)y=x4√x4+1(f)y=x−9√4x2+3x+2(g)y=12x−1(h)y=1logex(i)y=12x+1
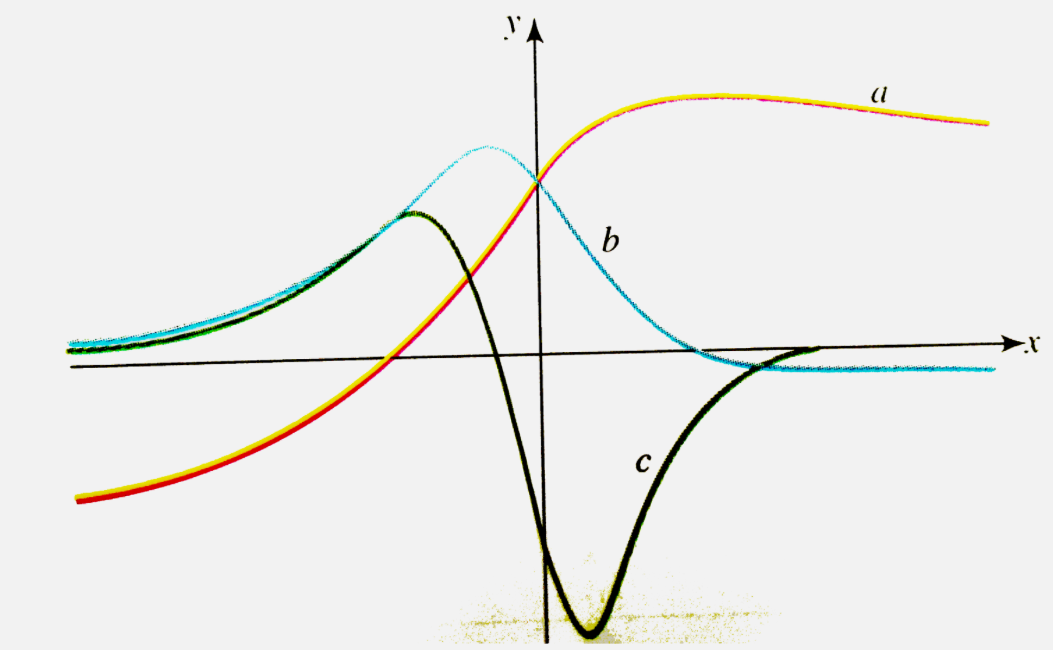
View SolutionThe figure shows the graphs of f, f' and f''. Indentify each curve and explain your choices.
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?

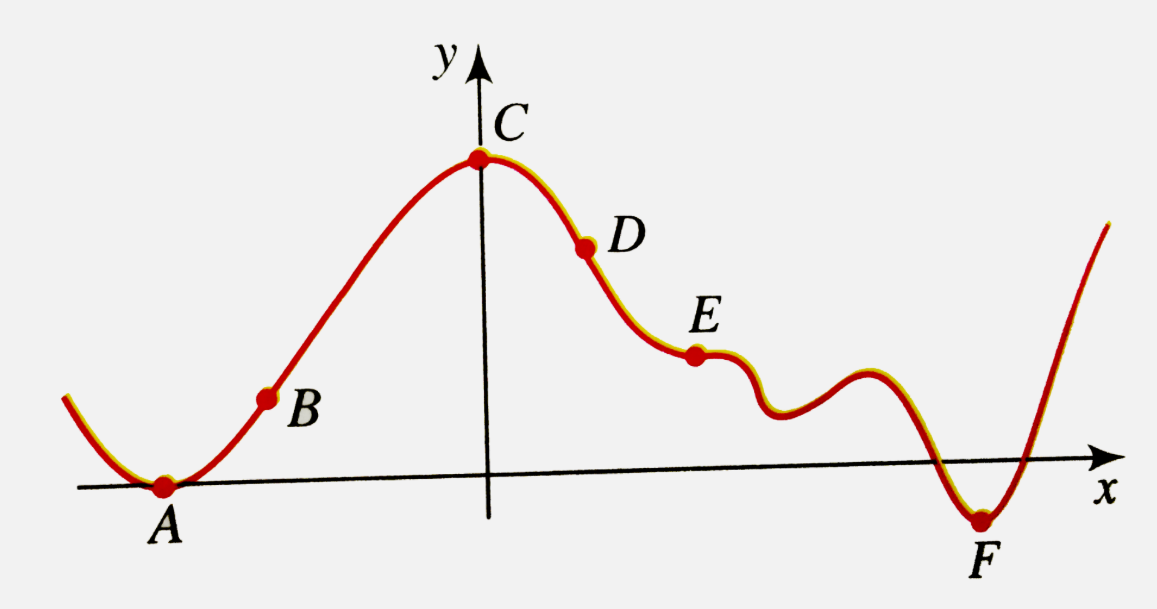
View SolutionThe graph of y = f(x) is given with six labelled points. Anser the following questions.
(a) At which point f'(x) has the greatest value?
(b) At which point f(x) and f'(x) both are zero?
(c) At how many point f'(x) is negative ?
(d) Which is the point of infection?
View SolutionThe graph of y=f(x) is given below
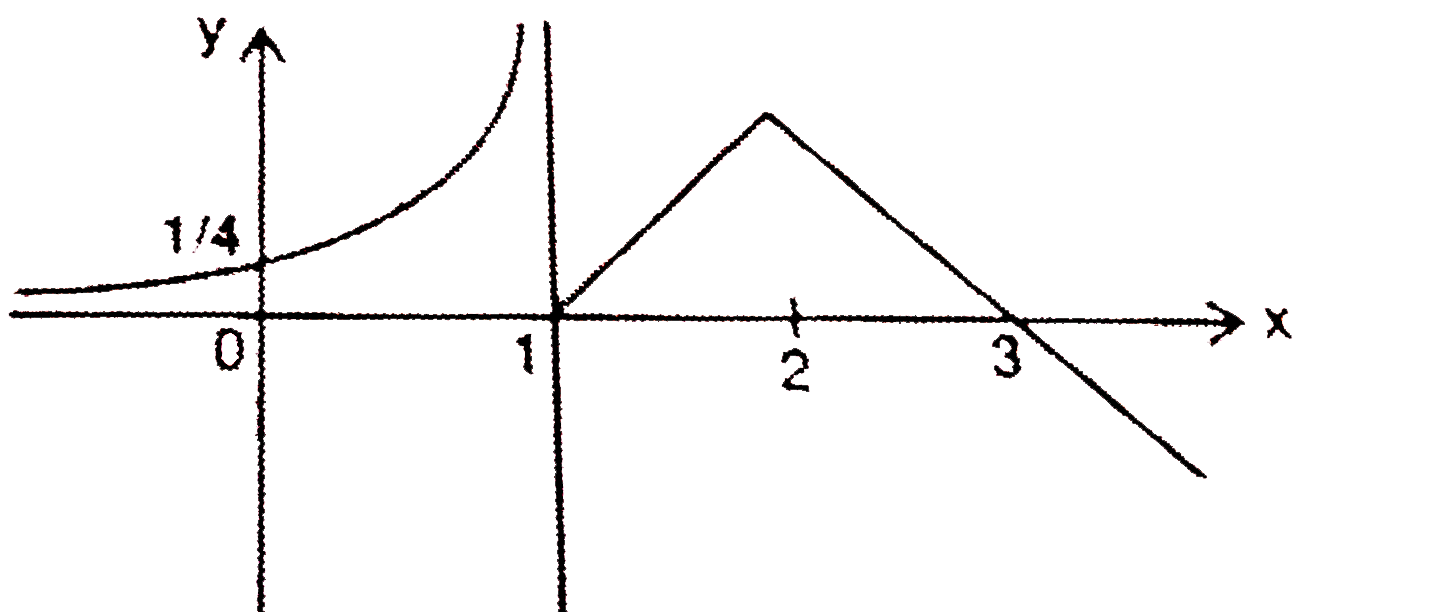
then the graph y=|f(|x|)| is :
View SolutionFollowing is the graph of y = f(x).
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_GRA_C01_S01_005_Q01.pngwh=80%mx-autosty≤=background:white;><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(a) Tangent line to y = f(x) at x = 0 makes an angle of sec−1√5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?

View SolutionThe graph of y = f(x) is given with six labelled points. Anser the following questions.
(a) At which point f'(x) has the greatest value?
(b) At which point f(x) and f'(x) both are zero?
(c) At how many point f'(x) is negative ?
(d) Which is the point of infection?

View SolutionThe graph of y =g(x) =f(X) is as shown in the following figure analyse this graph and answer the following question
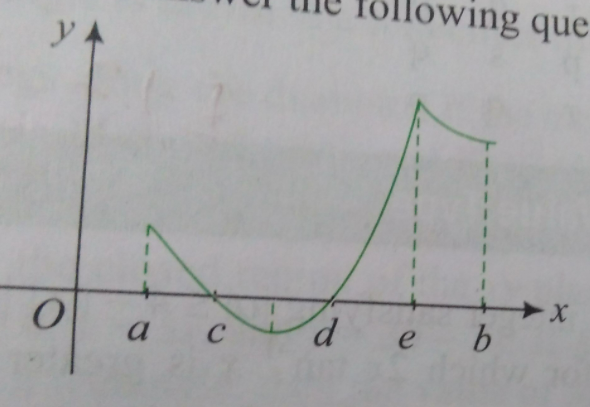
Number of points of inflectionn the graph of y = f(x) for a<x<b has
View SolutionThe graph of y=f(x) is given below

then the graph y=|f(|x|)| is :
View Solution
