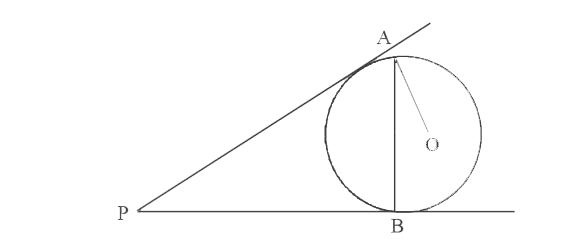
From a point P , two tangents PA and PB are drawn to a circle with centre O . If OP= diameter of the circle, show that APB is equilateral.
To show that triangle APB is equilateral when two tangents PA and PB are drawn from point P to a circle with center O, and OP is the diameter of the circle, we can follow these steps:
1. Identify the Elements:
- Let the radius of the circle be R.
- The diameter OP is given as 2R (since diameter = 2 × radius).
2. Draw the Tangents:
- Draw the circle with center O and radius R.
- From point P, draw the tangents PA and PB to the circle, touching the circle at points A and B respectively.
3. Join the Center to Points of Contact:
- Join OA and OB. Since OA and OB are radii of the circle, we have OA=OB=R.
4. Consider Triangles:
- Look at triangles △APO and △BPO.
- In both triangles, we have:
- OP as the hypotenuse (which is 2R).
- OA and OB as the perpendiculars (which are both R).
5. Apply the Sine Rule:
- For triangle △APO:
sin(θ)=OAOP=R2R=12
Thus, θ=30∘.
- For triangle △BPO:
sin(ϕ)=OBOP=R2R=12
Thus, ϕ=30∘.
6. Calculate Angle APB:
- The angle APB can be calculated as:
∠APB=θ+ϕ=30∘+30∘=60∘
7. Establish Equality of Tangents:
- Since PA and PB are tangents drawn from the same external point P, we have:
PA=PB
8. Use the Isosceles Triangle Property:
- In triangle APB, since PA=PB and ∠APB=60∘, we can conclude that:
∠PAB=∠PBA
- Let ∠PAB=∠PBA=x.
9. Sum of Angles in Triangle:
- The sum of angles in triangle APB gives:
∠APB+∠PAB+∠PBA=180∘
60∘+x+x=180∘
60∘+2x=180∘
2x=120∘⟹x=60∘
10. Conclusion:
- Since ∠PAB=∠PBA=60∘, we have:
∠APB=∠PAB=∠PBA=60∘
- Therefore, triangle APB is equilateral.
- Let the radius of the circle be R.
- The diameter OP is given as 2R (since diameter = 2 × radius).
- Draw the circle with center O and radius R.
- From point P, draw the tangents PA and PB to the circle, touching the circle at points A and B respectively.
- Join OA and OB. Since OA and OB are radii of the circle, we have OA=OB=R.
- Look at triangles △APO and △BPO.
- In both triangles, we have:
- OP as the hypotenuse (which is 2R).
- OA and OB as the perpendiculars (which are both R).
- For triangle △APO:
sin(θ)=OAOP=R2R=12
Thus, θ=30∘.
- For triangle △BPO:
sin(ϕ)=OBOP=R2R=12
Thus, ϕ=30∘.
- The angle APB can be calculated as:
∠APB=θ+ϕ=30∘+30∘=60∘
- Since PA and PB are tangents drawn from the same external point P, we have:
PA=PB
- In triangle APB, since PA=PB and ∠APB=60∘, we can conclude that:
∠PAB=∠PBA
- Let ∠PAB=∠PBA=x.
- The sum of angles in triangle APB gives:
∠APB+∠PAB+∠PBA=180∘
60∘+x+x=180∘
60∘+2x=180∘
2x=120∘⟹x=60∘
- Since ∠PAB=∠PBA=60∘, we have:
∠APB=∠PAB=∠PBA=60∘
- Therefore, triangle APB is equilateral.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
A45∘B90∘C30∘D60∘ - Question 2 - Select One
From a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then ∠APB is
A60∘B45∘C90∘D30∘
From a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.
 View Solution
View SolutionFrom a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT=120∘ Prove that OP = 2PS.
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
 View Solution
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
 View Solution
View Solution

