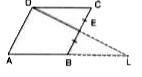
From the given diagram, in which ABCD is a parallelgram, ABL is a line segment and E is mid point of BC. Prove that :
(i) ΔDCE≅ΔLBE
(ii) AB = BL
(iii) AL = 2DC
Step by step video & image solution for From the given diagram, in which ABCD is a parallelgram, ABL is a line segment and E is mid point of BC. Prove that : (i) Delta DCE ~= Delta LBE (ii) AB = BL (iii) AL = 2DC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - EXERCISE 9(B)
20 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
From the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
ΔDCE≅ΔLBE

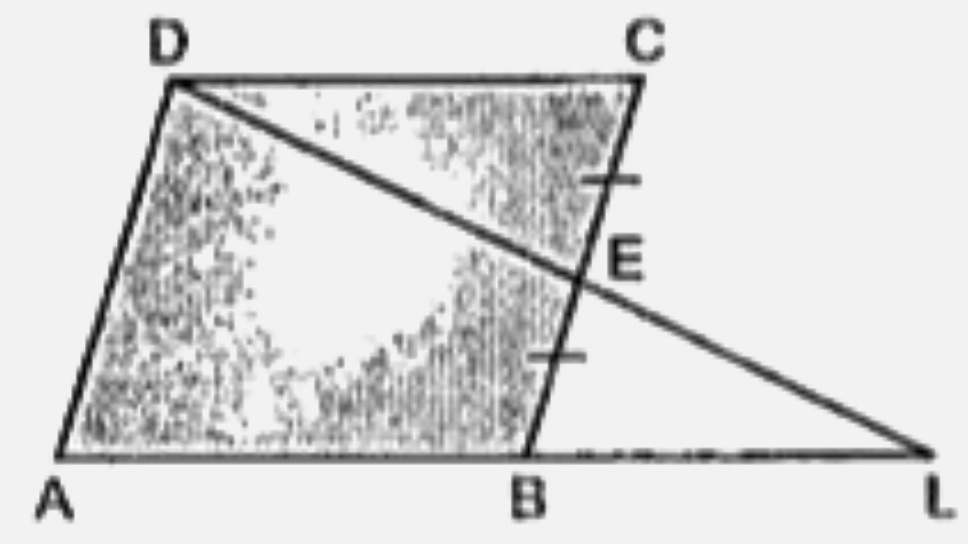
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AB=BL
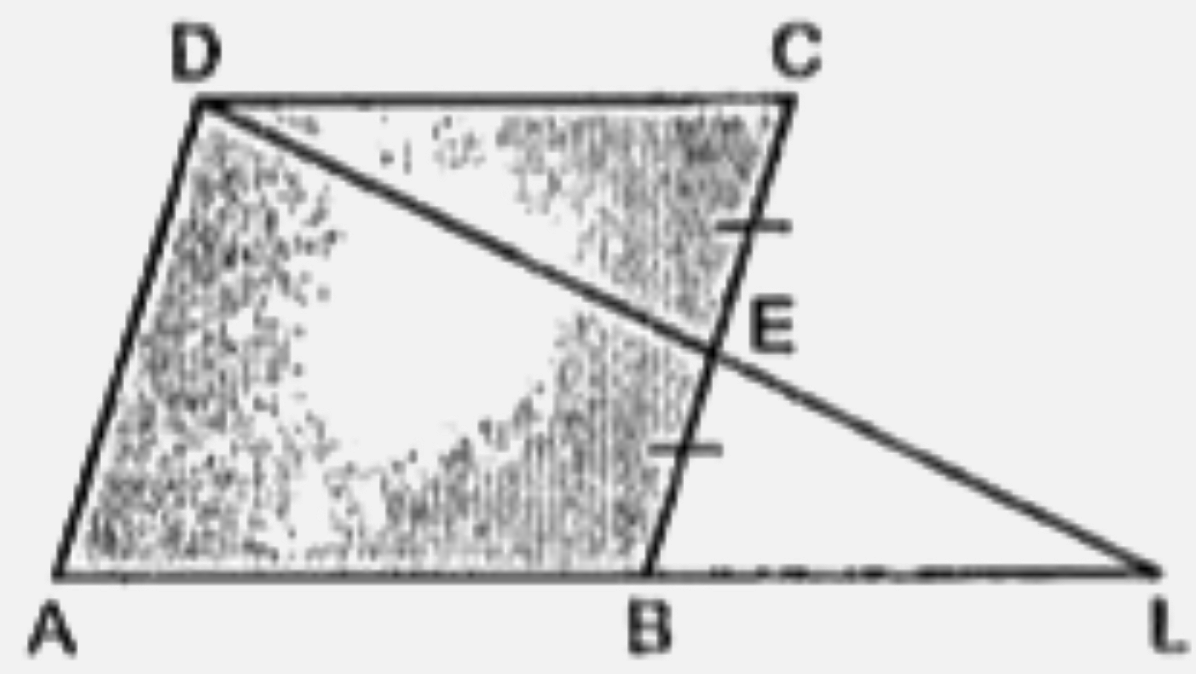
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AL=2DC
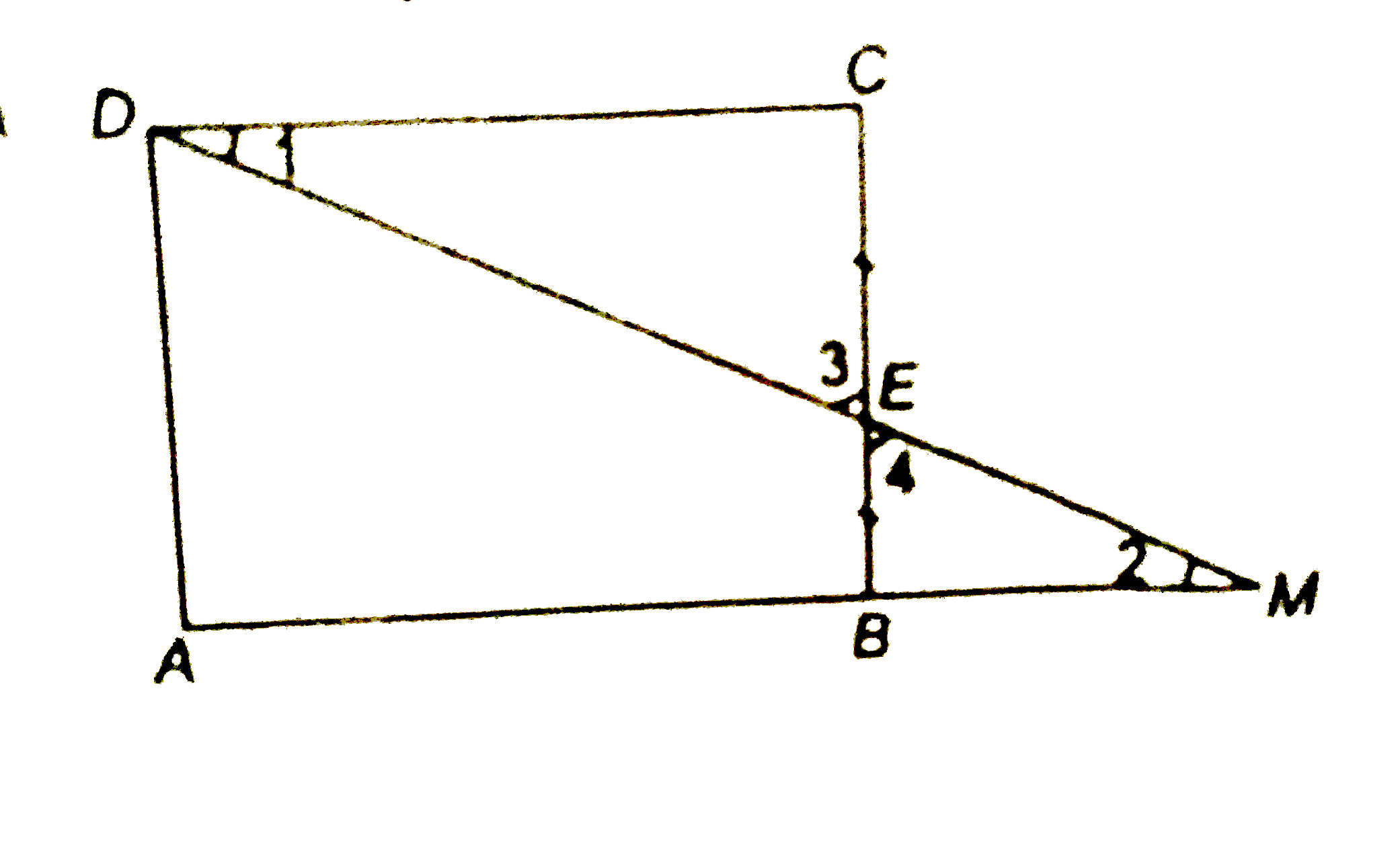
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
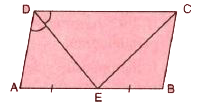
BC= BE
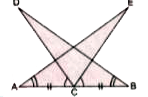
View SolutionUse the information given in the adjoining figure, to prove :
(i) ΔDBC≅ΔEAC.
(ii) DC = EC.
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.
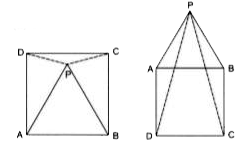
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View Solution
