Give two circles intersecting orthogonally having the length of common chord $24 / 5$ units. The radius of one of the circles is 3 units.
The radius of other circle is

A

6 units

B

4 units

C

2 units

D

4units

Text Solution

Verified by Experts

The correct Answer is:2

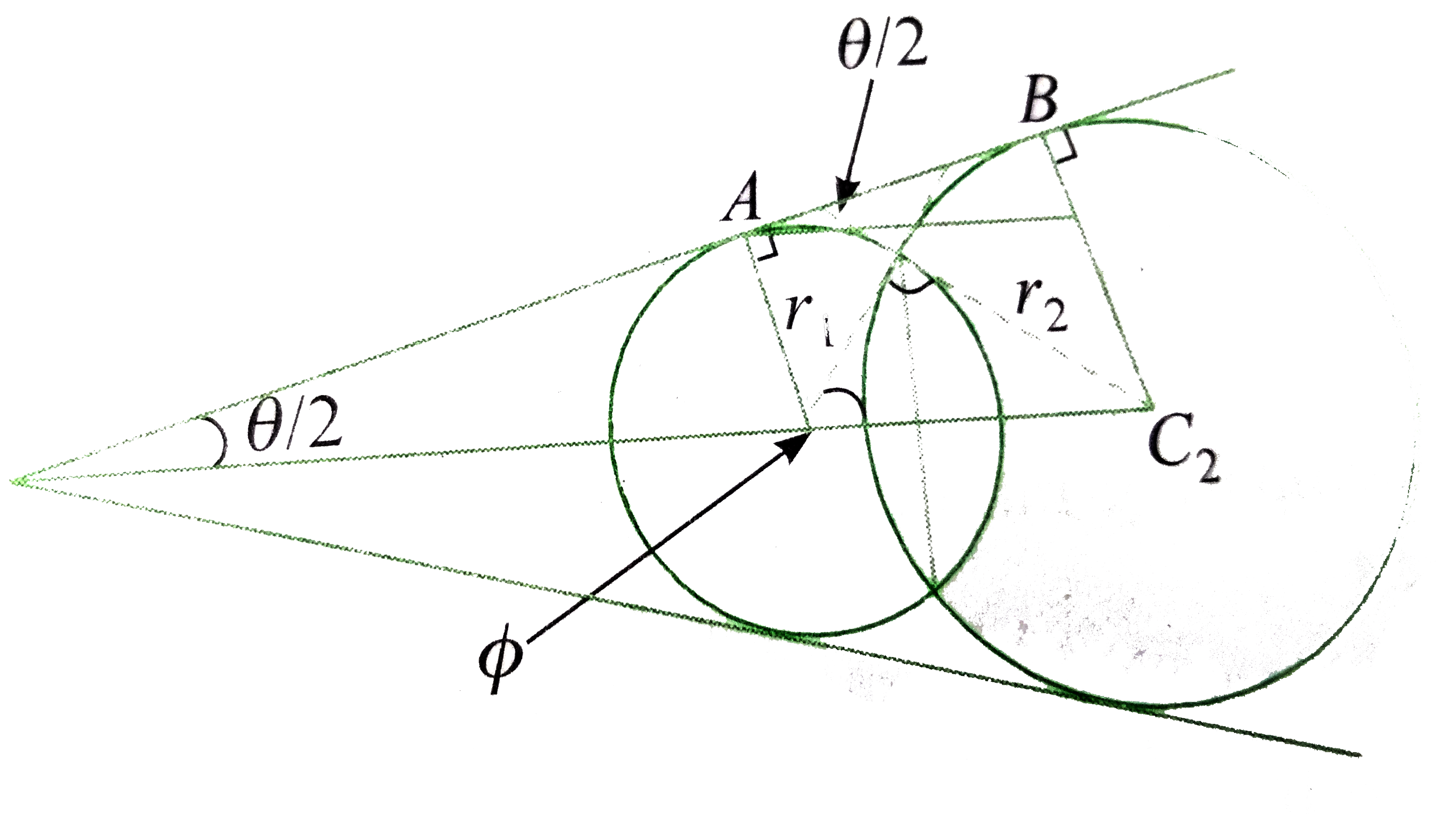
We have $sin ϕ = d / r_{1}$ and $cos ϕ = d / r_{2}$ . ( where 2d is the length of the comon chord ). Then,
$l = \frac{d^{2}}{r_{1}^{2}} + \frac{d^{2}}{r_{2}^{2}}$
or $d = \frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
or $2 d = \frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}} = \frac{24}{5},$ where $r_{1} = 3$
or $d = \frac{6 r_{2}}{\sqrt{9 + r_{2}^{2}}} = \frac{24}{5}$
or $r_{2} = 4$
From the figure,
$sin . \frac{θ}{2} = \frac{r_{2} - r_{1}}{C_{1} C_{2}}$
where $C_{1}^{2} C_{2}^{2} = r_{1}^{2} + r_{2}^{2}$
or $C_{1} C_{2} = 5$
$∴ sin . \frac{θ}{2} = \frac{1}{5}$
or $cos . \frac{θ}{2} = \frac{\sqrt{24}}{5}$
$∴ sin θ = 2 x \frac{1}{5} \times \frac{\sqrt{24}}{5}$
$= \frac{4 \sqrt{6}}{25}$
or $θ = {sin}^{- 1} . \frac{4 \sqrt{6}}{25}$
Also, $A B = \sqrt{C_{1} C_{2}^{2} - {(r_{1} - r_{2})}_{1}^{2}} = \sqrt{25 - 1} = \sqrt{24}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Give two circles intersecting orthogonally having the length of common chord $24 / 5$ units. The radius of one of the circles is 3 units.
The length of direct common tangent is
A $\sqrt{12}$
B $4 \sqrt{3}$
C $2 \sqrt{6}$
D $3 \sqrt{6}$
Question 2 - Select One
Give two circles intersecting orthogonally having the length of common chord $24 / 5$ units. The radius of one of the circles is 3 units.
The angle between direct common tangents is
A ${sin}^{- 1} . \frac{24}{25}$
B ${sin}^{- 1} . \frac{4 \sqrt{6}}{25}$
C ${sin}^{- 1} . \frac{4}{5}$
D ${sin}^{- 1} . \frac{12}{25}$
Question 3 - Select One
Given two circles intersecting orthogonally having the length of common chord $\frac{24}{5}$ unit. The radius of one of the circles is 3 units.
If length of direct common tangent is $λ$ units, then $λ^{2}$ is
A12
B24
C36
D48

CENGAGE-CIRCLE -Exercise (Comprehension)

Home
Ask Doubt
Profile