If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, then prove that PA is angle bisector of ∠BPC.
To prove that line segment PA is the angle bisector of angle BPC in an equilateral triangle ABC inscribed in a circle, follow these steps:
1. Draw the Figure: Start by drawing an equilateral triangle ABC inscribed in a circle with center O. Mark point P on the minor arc BC, ensuring that P does not coincide with points B or C.
2. Identify Angles: We need to prove that PA bisects angle BPC. Let angle BPC be divided into two angles: angle 1 (∠APB) and angle 2 (∠APC).
3. Use Properties of the Circle: Since ABC is an equilateral triangle, the angles at the center of the circle can be expressed as:
- Angle AOB = Angle AOC = Angle BOC = 120° (since each angle in an equilateral triangle is 60° and the central angle is twice that).
4. Relate Angles at the Center to Angles at Point P:
- By the inscribed angle theorem, the angles subtended by the same arc at the circumference are equal to half the angle subtended at the center. Therefore:
- Angle APB = 1/2 * Angle AOB
- Angle APC = 1/2 * Angle AOC
5. Substitute the Known Angles: Since Angle AOB = Angle AOC, we can denote this common angle as θ. Thus:
- Angle APB = 1/2 * θ
- Angle APC = 1/2 * θ
6. Equate the Angles: Since both angles APB and APC are equal to half of the same angle θ, we have:
- Angle 1 (∠APB) = 1/2 * Angle AOB
- Angle 2 (∠APC) = 1/2 * Angle AOC
- Therefore, Angle 1 = Angle 2
7. Conclude the Proof: Since angle 1 is equal to angle 2, we conclude that PA is the angle bisector of angle BPC.
Final Statement:
Thus, we have proved that PA is the angle bisector of angle BPC.
---
- Angle AOB = Angle AOC = Angle BOC = 120° (since each angle in an equilateral triangle is 60° and the central angle is twice that).
- By the inscribed angle theorem, the angles subtended by the same arc at the circumference are equal to half the angle subtended at the center. Therefore:
- Angle APB = 1/2 * Angle AOB
- Angle APC = 1/2 * Angle AOC
- Angle APB = 1/2 * θ
- Angle APC = 1/2 * θ
- Angle 1 (∠APB) = 1/2 * Angle AOB
- Angle 2 (∠APC) = 1/2 * Angle AOC
- Therefore, Angle 1 = Angle 2
Thus, we have proved that PA is the angle bisector of angle BPC.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
In Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
View SolutionIn Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
View SolutionABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
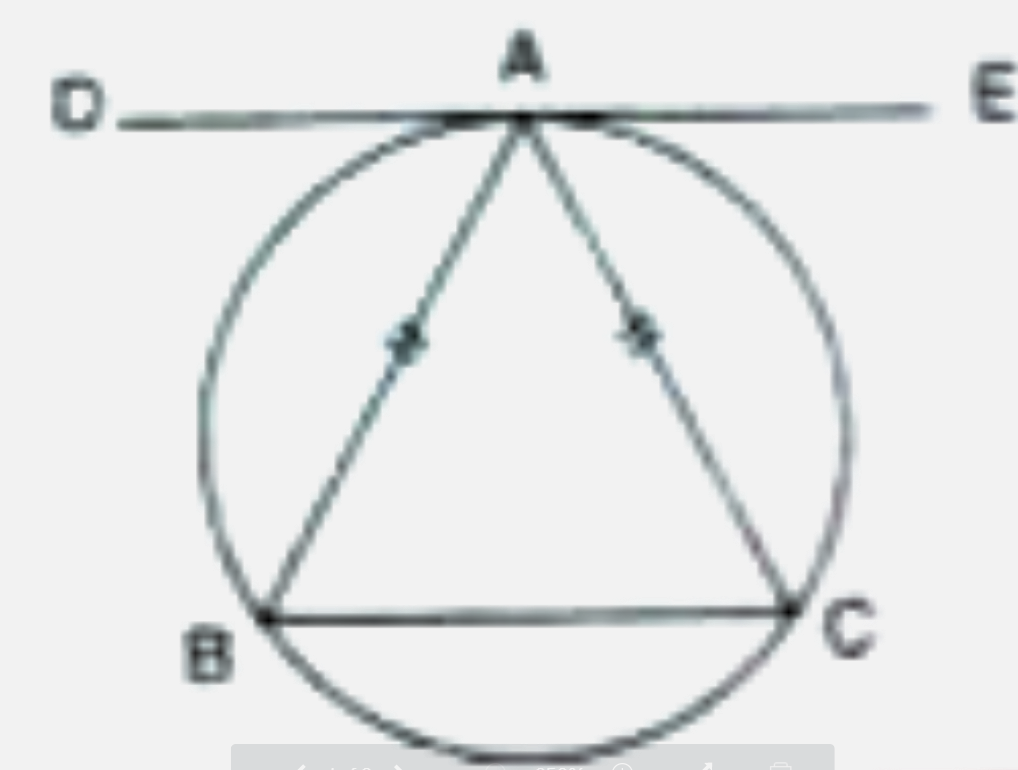
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
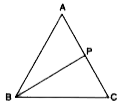
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC

View SolutionABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
View SolutionIf in a ΔABC, cotA+cotB+cotC=√3 . Prove that triangle is equilateral
View Solution
