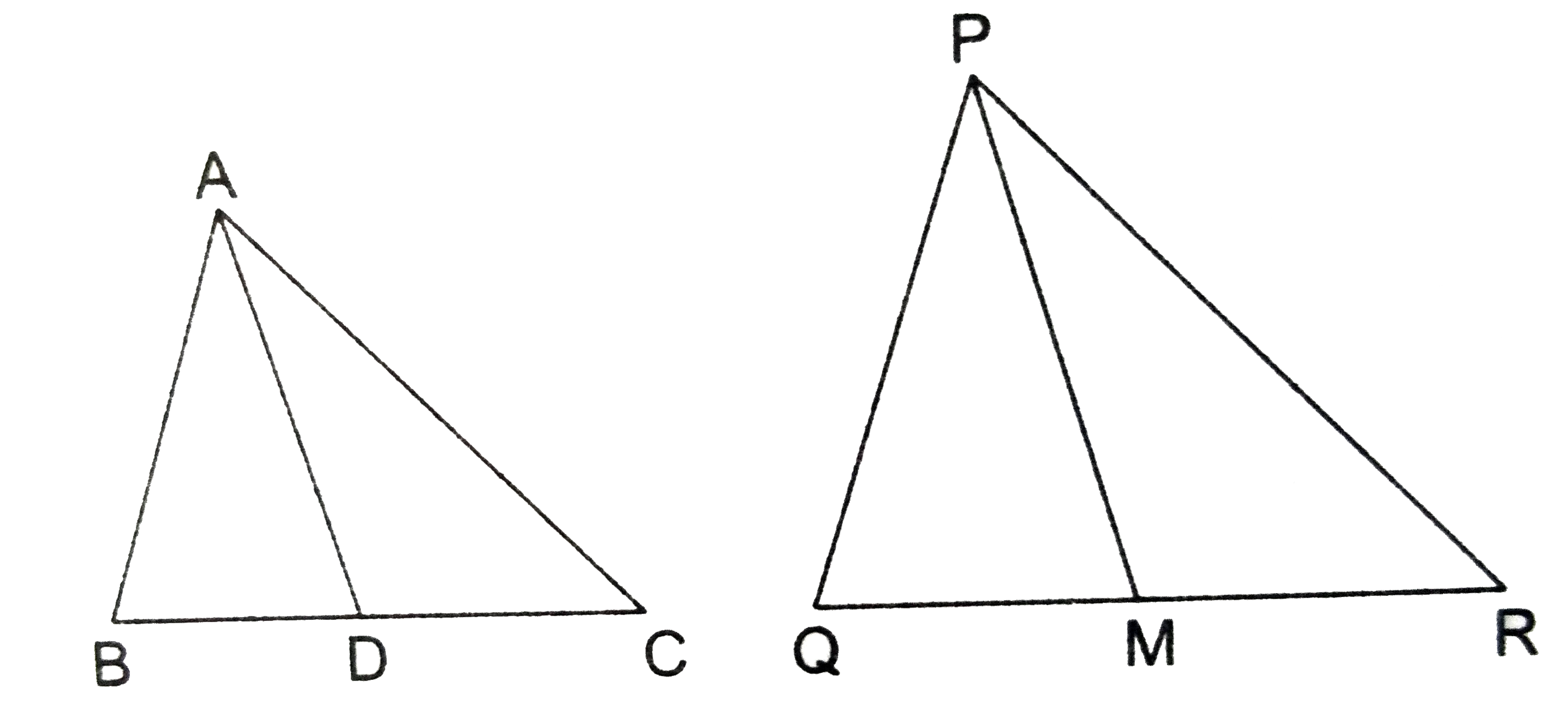
If AD and PM are medians of triangles ABC and PQR, respectively whereΔABCΔPQR, prove that ABPQ=ADPM
Step by step video solution for If AD and PM are medians of triangles ABC and PQR, respectively whereDeltaA B C DeltaP Q R, prove that (A B)/(P Q)=(A D)/(P M) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]EXERCISE - SECTION - D12videos
SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]EXERCISE - SECTION - B7videos
SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2019EXERCISE - Section - D12videos
SAMPLE PAPER 2019
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-V)5videos
SAMPLE PAPER 4
Similar Questions
If AD and PM are medians of triangles ABC and PQR, respectively whereΔABC~ΔPQR, prove that ABPQ=ADPM
View SolutionAD and PM are medians of triangles ABC and PQR respectively where ΔABC~ΔPQR. Prove that: ABPQ=ADPM.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
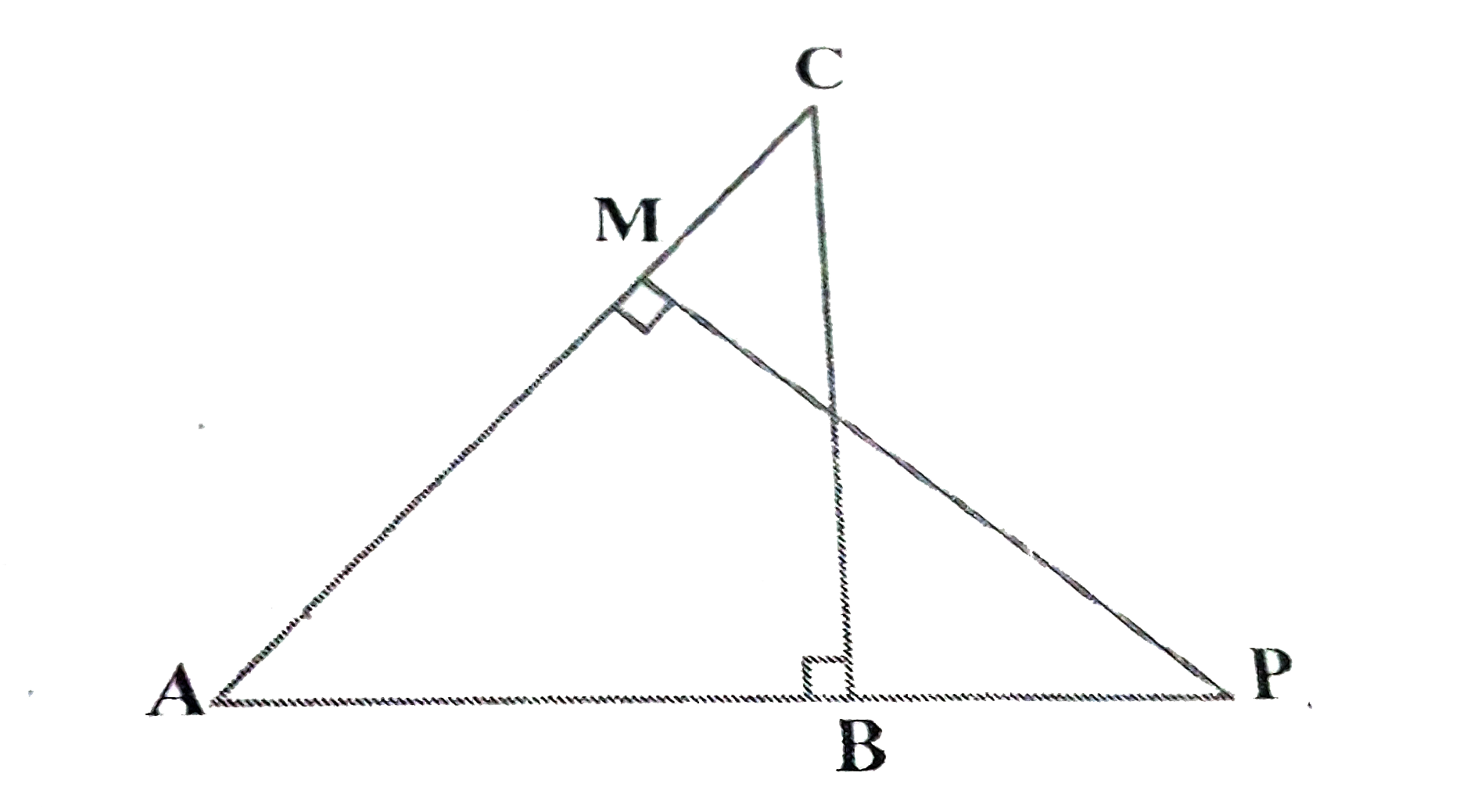 View Solution
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ
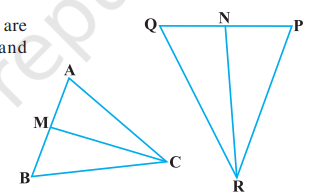 View Solution
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
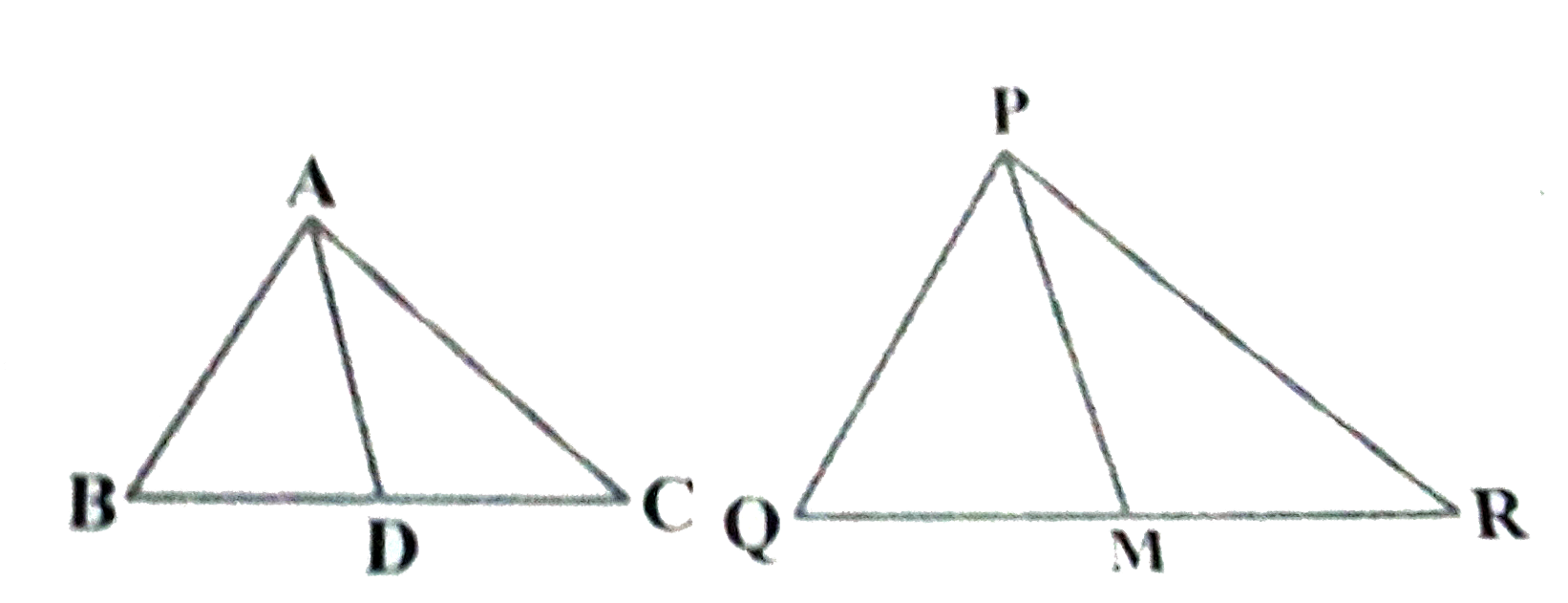 View Solution
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
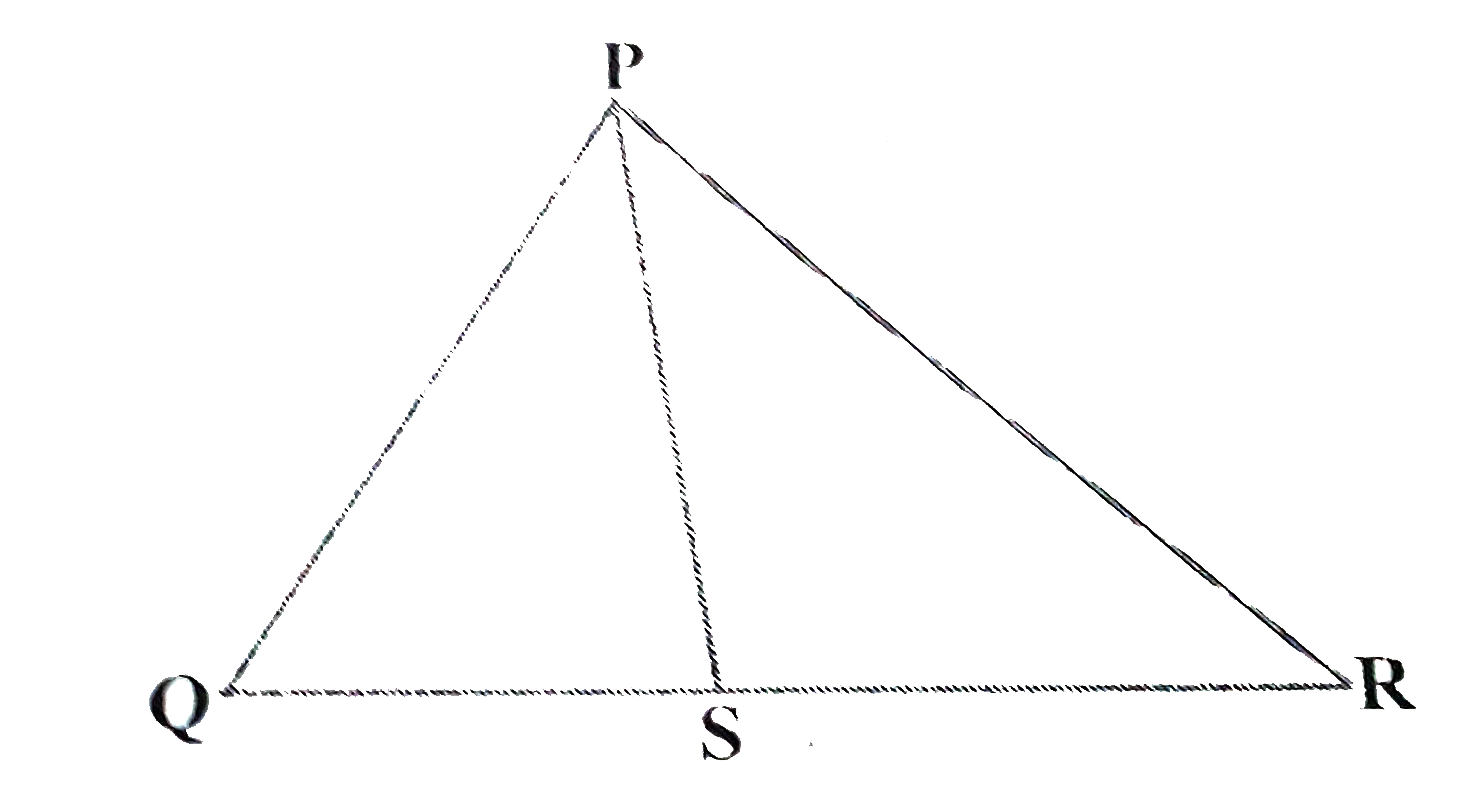 View Solution
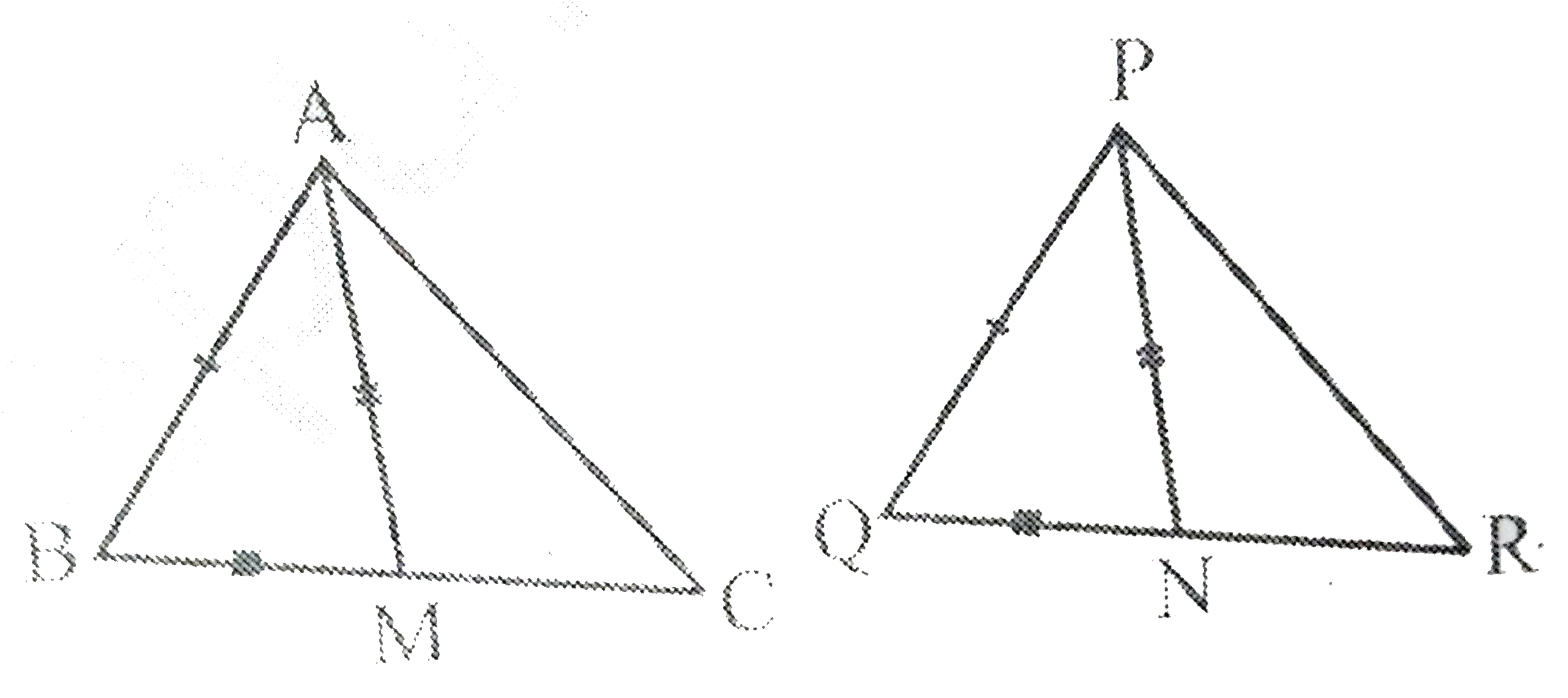
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
 View Solution
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution

