In a parallelogram ABCD, point P lies in DC such that DP:PC= 3:2. If area of ΔDPB=30sq. cm, ffind the area of the parallelogram ABCD.
The correct Answer is:100cm2
To find the area of the parallelogram ABCD given that point P lies on DC such that DP:PC = 3:2 and the area of triangle DPB is 30 cm², we can follow these steps:
1. Understanding the Ratios:
- We know that DP:PC = 3:2. This means if we let DP = 3x and PC = 2x for some value x, then the total length of DC = DP + PC = 3x + 2x = 5x.
2. Area of Triangle DPB:
- The area of triangle DPB is given as 30 cm². We can denote the height from point B to line DC as h1.
3. Finding Area of Triangle BPC:
- Since the triangles DPB and BPC share the same height (h1) from point B to line DC, we can express the area of triangle BPC in terms of its base PC.
- The area of triangle BPC can be calculated using the ratio of the bases:
Area of △DPBArea of △BPC=DPPC
- Substituting the known values:
30Area of △BPC=32
- Cross-multiplying gives:
3⋅Area of △BPC=30⋅2
3⋅Area of △BPC=60
Area of △BPC=603=20 cm2
4. Finding Area of Triangle BDC:
- The area of triangle BDC can be found by adding the areas of triangles DPB and BPC:
Area of △BDC=Area of △DPB+Area of △BPC
Area of △BDC=30 cm2+20 cm2=50 cm2
5. Finding Area of Parallelogram ABCD:
- The area of parallelogram ABCD is twice the area of triangle BDC (since diagonal BD divides the parallelogram into two equal areas):
Area of parallelogram ABCD=2×Area of △BDC
Area of parallelogram ABCD=2×50 cm2=100 cm2
Final Answer:
The area of parallelogram ABCD is 100 cm².
- We know that DP:PC = 3:2. This means if we let DP = 3x and PC = 2x for some value x, then the total length of DC = DP + PC = 3x + 2x = 5x.
- The area of triangle DPB is given as 30 cm². We can denote the height from point B to line DC as h1.
- Since the triangles DPB and BPC share the same height (h1) from point B to line DC, we can express the area of triangle BPC in terms of its base PC.
- The area of triangle BPC can be calculated using the ratio of the bases:
Area of △DPBArea of △BPC=DPPC
- Substituting the known values:
30Area of △BPC=32
- Cross-multiplying gives:
3⋅Area of △BPC=30⋅2
3⋅Area of △BPC=60
Area of △BPC=603=20 cm2
- The area of triangle BDC can be found by adding the areas of triangles DPB and BPC:
Area of △BDC=Area of △DPB+Area of △BPC
Area of △BDC=30 cm2+20 cm2=50 cm2
- The area of parallelogram ABCD is twice the area of triangle BDC (since diagonal BD divides the parallelogram into two equal areas):
Area of parallelogram ABCD=2×Area of △BDC
Area of parallelogram ABCD=2×50 cm2=100 cm2
The area of parallelogram ABCD is 100 cm².
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
Knowledge Check

In the figure above, what is the area of parallelogram ABCD?A4√2B4√3C6√2D6√3
ABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
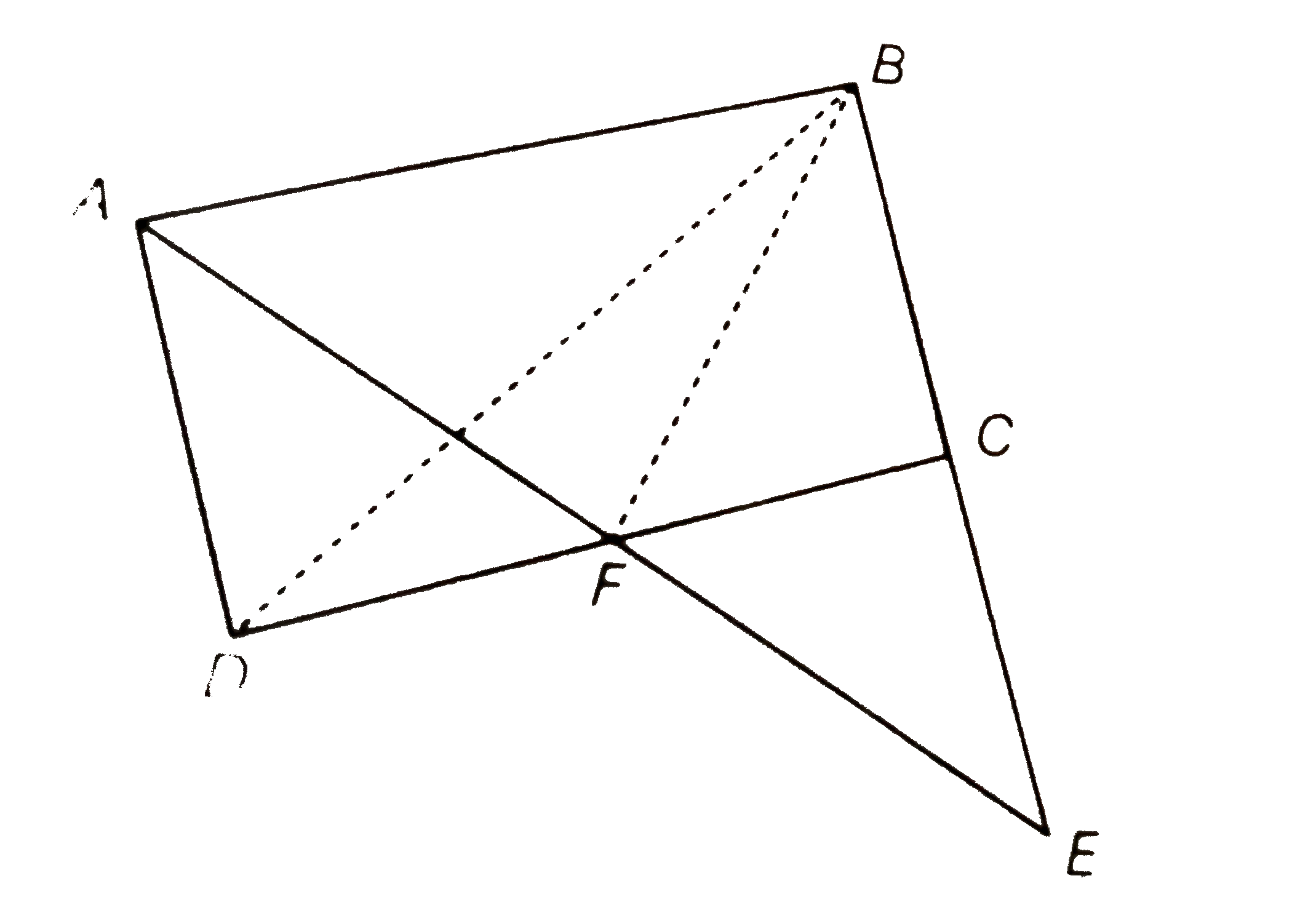
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If ar.(ΔDFB)=30cm2, find the area of parallelogram
View SolutionABCD is a parallelogram whose adjacent sides AB = 48 cm and BC = 14 cm . One of its diagonds AC = 50 cm . Find :
(i) the area of the parallelogram ABCD.
(ii) the distance between the longer sides.
(iii) the distance between the shorter sides.
View SolutionIn the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2
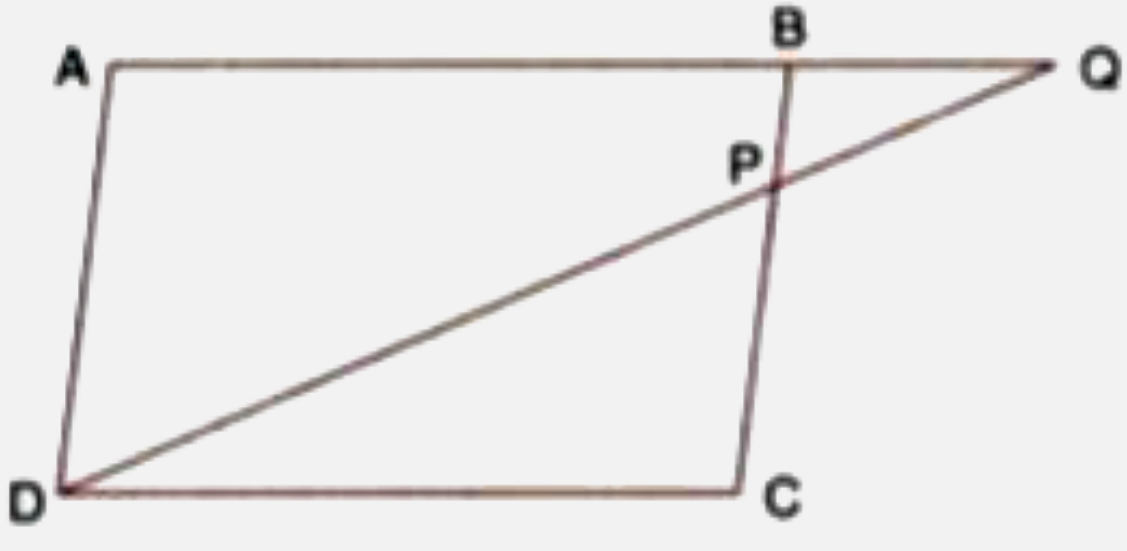
Calculate :
area of parallelogram ABCD.
View SolutionThree vertices of a parallelogram ABCD are A(3,−4),B(−1,−3)andC(−6,2). Find the coordinates of vertiex D and find the area of parallelogram ABCD.
View Solution