In a rectangle ABCD , E is the mid -point of AB . If AB= 16 m and AD = 6 m , then find ED .
15 cm
10 cm
12 m
14 m
The correct Answer is:B
To find the length of ED in rectangle ABCD, where E is the midpoint of AB, we can follow these steps:
1. Identify the Dimensions of the Rectangle:
- Given that AB = 16 m and AD = 6 m, we can label the rectangle ABCD accordingly.
- Therefore, AB = CD = 16 m and AD = BC = 6 m.
2. Locate Point E:
- Since E is the midpoint of AB, we can find AE and EB.
- AE = EB = AB/2 = 16 m / 2 = 8 m.
3. Draw Triangle AED:
- We will now consider triangle AED. The lengths we have are:
- AE = 8 m (from step 2)
- AD = 6 m (given)
4. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem, in right triangle AED:
AD2+AE2=ED2
- Plugging in the values:
62+82=ED2
36+64=ED2
100=ED2
5. Calculate ED:
- To find ED, take the square root of both sides:
ED=√100=10 m
Final Answer:
ED = 10 m
---
- Given that AB = 16 m and AD = 6 m, we can label the rectangle ABCD accordingly.
- Therefore, AB = CD = 16 m and AD = BC = 6 m.
- Since E is the midpoint of AB, we can find AE and EB.
- AE = EB = AB/2 = 16 m / 2 = 8 m.
- We will now consider triangle AED. The lengths we have are:
- AE = 8 m (from step 2)
- AD = 6 m (given)
- According to the Pythagorean theorem, in right triangle AED:
AD2+AE2=ED2
- Plugging in the values:
62+82=ED2
36+64=ED2
100=ED2
- To find ED, take the square root of both sides:
ED=√100=10 m
ED = 10 m
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -2)15videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Match the following )3videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6 .612videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
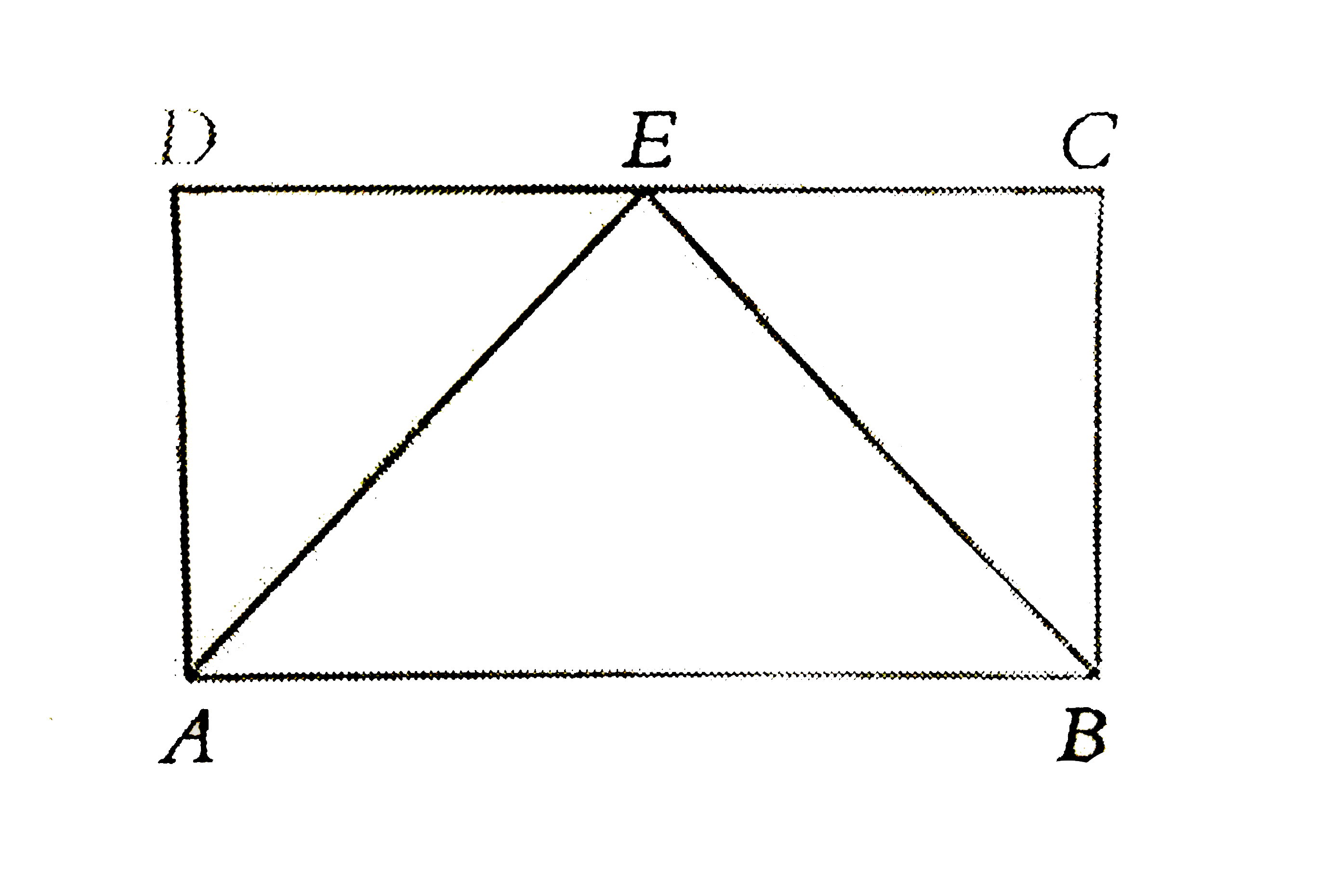
In the figure above ( not to scale ), ABCD is a rectangle, E is the mid - point of CD. If CD=24 cm and AD=5 cm, then find the perimeter of ΔABE.View Solution
In the figure above ( not to scale ), ABCD is a rectangle, E is the mid - point of CD. If CD=24 cm and AD=5 cm, then find the perimeter of ΔABE.View Solution
Knowledge Check
- Question 1 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC - Question 2 - Select One
In a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A1/2(□ABCD)B1/3(□ABCD)C1/4(□ABCD)Dnone of these - Question 3 - Select One
In a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A12(□ABCD)B13(□ABCD)C14(□ABCD)Dnone of these
Point M is the mid point of seg AB and AB = 14 unit then AM =?
View SolutionIn a rectangle ABCD, E is the midpoint of AB, F is point on AC such that BF is perpendicular to AC and FE perpendicular to BD. Suppose BC=8√3. Find AB
View SolutionIn the adjoining figure
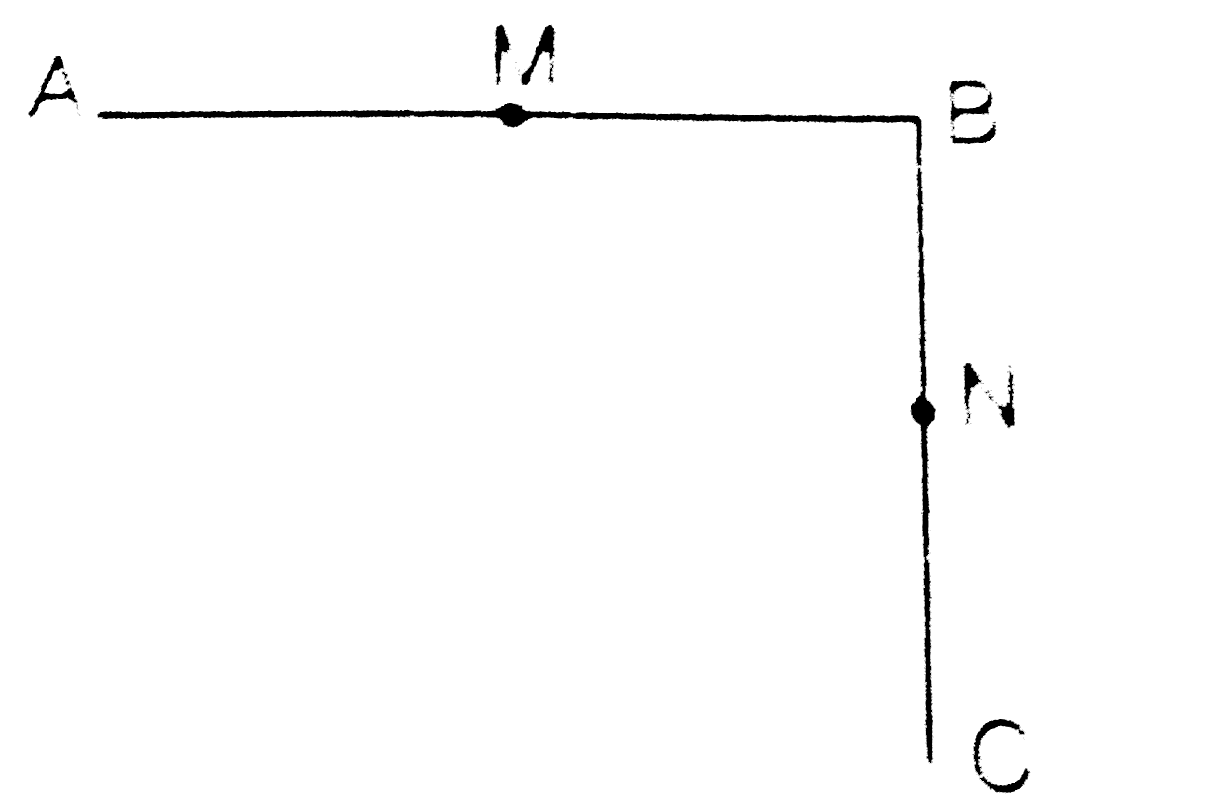
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.View Solution△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
View SolutionIf ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
View Solution

