In a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠POC=(2212)∘
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Draw the Square
We start by drawing square ABCD where:
- A is the top left corner,
- B is the top right corner,
- C is the bottom right corner,
- D is the bottom left corner.
Step 2: Identify the Diagonals
Draw the diagonals AC and BD. They intersect at point O, which is the center of the square. Since ABCD is a square, the diagonals bisect each other at right angles (90 degrees).
Step 3: Mark Point P
Place point P on side BC such that OB = BP. This means that P divides side BC into two equal segments.
Step 4: Analyze Triangle OBP
In triangle OBP:
- Since OB = BP, triangle OBP is isosceles.
- The angle at B (angle OBP) is 90 degrees (since diagonals bisect at right angles).
- Therefore, angle OBP = angle OBP = 45 degrees (since the angles opposite the equal sides are equal).
Step 5: Calculate Angle BOP
Using the triangle sum property:
- The sum of angles in triangle OBP = 180 degrees.
- We have angle OBP = 45 degrees and angle OBP = 45 degrees.
- Therefore, angle BOP = 180 - (45 + 45) = 90 degrees.
Step 6: Calculate Angle BOC
Since diagonals bisect each other at right angles:
- Angle BOC = 90 degrees.
Step 7: Calculate Angle POC
Now, we can find angle POC:
- Angle POC = Angle BOC - Angle BOP.
- Substitute the values: Angle POC = 90 degrees - 67.5 degrees.
Step 8: Final Calculation
- Angle POC = 90 - 67.5 = 22.5 degrees.
- This can also be expressed as 22 1/2 degrees.
Conclusion
We have shown that angle POC = 22 1/2 degrees as required.
We start by drawing square ABCD where:
- A is the top left corner,
- B is the top right corner,
- C is the bottom right corner,
- D is the bottom left corner.
Draw the diagonals AC and BD. They intersect at point O, which is the center of the square. Since ABCD is a square, the diagonals bisect each other at right angles (90 degrees).
Place point P on side BC such that OB = BP. This means that P divides side BC into two equal segments.
In triangle OBP:
- Since OB = BP, triangle OBP is isosceles.
- The angle at B (angle OBP) is 90 degrees (since diagonals bisect at right angles).
- Therefore, angle OBP = angle OBP = 45 degrees (since the angles opposite the equal sides are equal).
Using the triangle sum property:
- The sum of angles in triangle OBP = 180 degrees.
- We have angle OBP = 45 degrees and angle OBP = 45 degrees.
- Therefore, angle BOP = 180 - (45 + 45) = 90 degrees.
Since diagonals bisect each other at right angles:
- Angle BOC = 90 degrees.
Now, we can find angle POC:
- Angle POC = Angle BOC - Angle BOP.
- Substitute the values: Angle POC = 90 degrees - 67.5 degrees.
- Angle POC = 90 - 67.5 = 22.5 degrees.
- This can also be expressed as 22 1/2 degrees.
We have shown that angle POC = 22 1/2 degrees as required.
Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(C )
28 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 3 MARKS QUESTIONS
5 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B) (true/false)
10 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
In a square ABCD, diagonals meet at O. P is point on BC such that OB = BP.Show that (i) ∠POC=(2212)∘
(ii) ∠BDC=2∠POC
(iii) ∠BOP=3∠COP
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BDC=2∠POC
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BOP=3∠COP
View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View SolutionABC is an equilateral triangle, P is a point in BC such that BP : PC =2 : 1.
Prove that : 9AP2=7AB2
View SolutionA point O lies inside a ΔABC. Show that OA+OB+OC>12(AB+BC+CA).
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2
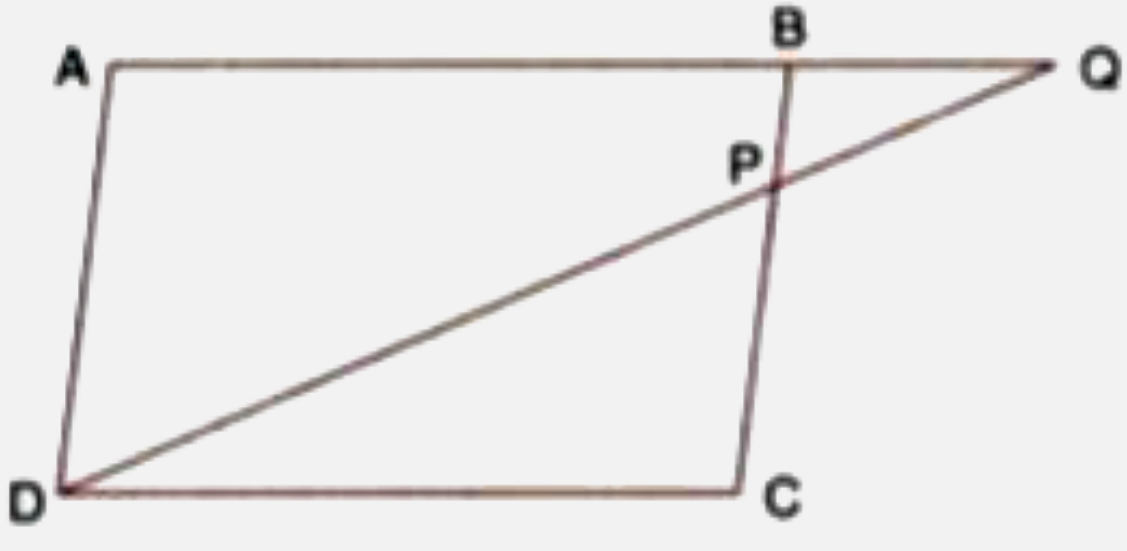
Calculate :
area of parallelogram ABCD.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2

Calculate :
area of triangle CDP.
View SolutionABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP : area of trapezium APCD = 1:5. Find the length of CP.
View Solution
