In a triangle ABC median AD is produced to X such that AD=DX. Prove that ABXC is a parallelogram.
In quadrilateral ABXC, we have
AD=DX(Given
BD=DC(Given)
So, diagonals AXand BC bisect each other.
Therefore,ABXC is a parallelogram.
∠BDA=∠CDX
△ABD≈△XCD
XC=AB
∠ABC=∠XCB
These two angles form a pair of alternate angles.
AB∣∣CX
Now, as two opposite sides are parallel and equal, we can say that ABXC is a parallelogram.
Topper's Solved these Questions
Similar Questions
In a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
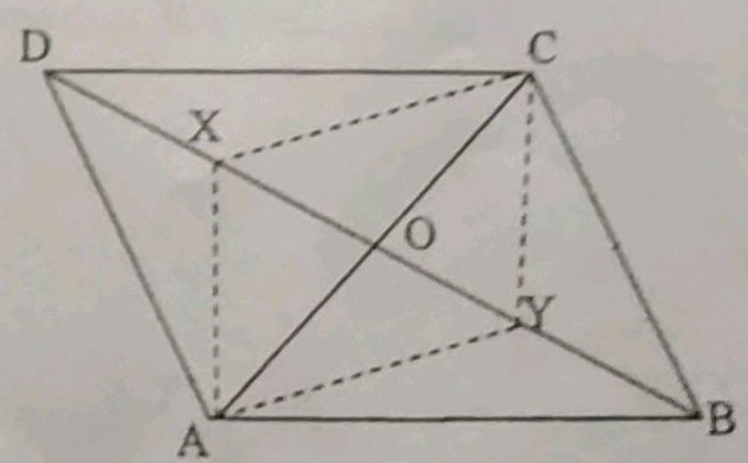 View Solution
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
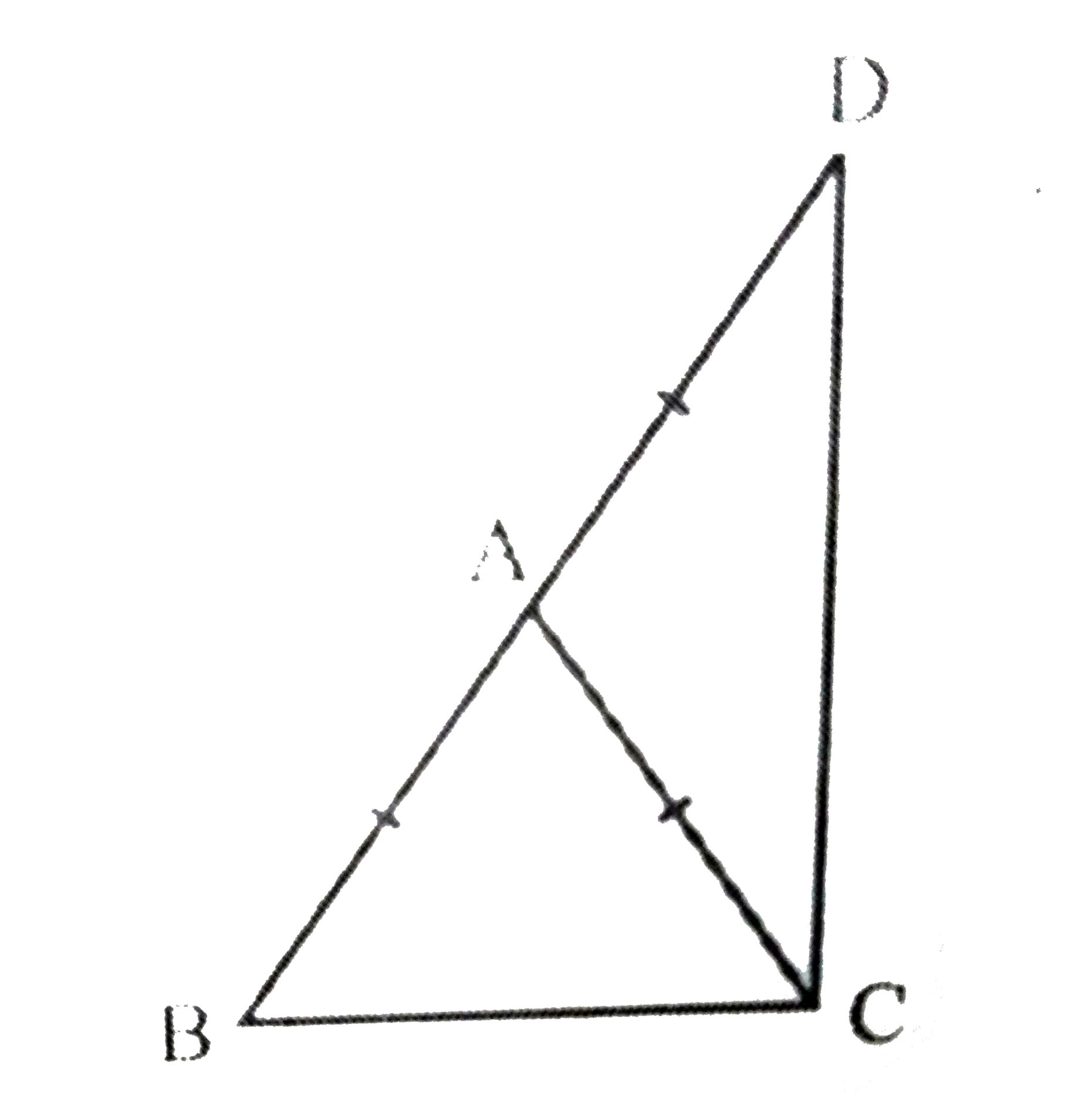 View Solution
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
 View Solution
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View Solution

