In a △ ABC,AB=2,BC=4,CA=3. If D is the mid-point of BC, then the correct statement(s) is/are
cosB≠1116
cosC≠78
AD≠2.4
AD2=2.5
To solve the problem, we need to analyze the triangle ABC with the given sides AB=2, BC=4, and CA=3. We also need to find the midpoint D of side BC and evaluate the given statements.
1. Draw Triangle ABC:
- Let A, B, and C be the vertices of the triangle.
- Place B at the origin (0,0) and C at (4,0) since BC=4.
- To find the coordinates of A, we can use the distances from B and C.
2. Find Coordinates of Point A:
- The distance AB=2 gives us the equation:
√x2A+y2A=2(1)
- The distance AC=3 gives us the equation:
√(xA−4)2+y2A=3(2)
- Squaring both equations:
- From (1): x2A+y2A=4
- From (2): (xA−4)2+y2A=9
3. Expand and Simplify Equation (2):
- Expanding (2):
x2A−8xA+16+y2A=9
- Substitute x2A+y2A=4 into the equation:
4−8xA+16=9
- Simplifying gives:
−8xA+20=9⟹−8xA=−11⟹xA=118
4. Substitute xA back to find yA:
- Using x2A+y2A=4:
(118)2+y2A=4
12164+y2A=4⟹y2A=4−12164=256−12164=13564
- Thus, yA=±√13564=±√1358=±3√158.
5. Find Midpoint D of BC:
- The coordinates of D (midpoint of BC):
D=(0+42,0+02)=(2,0)
6. Calculate AD:
- The length AD can be calculated using the distance formula:
AD=
⎷(118−2)2+(3√158)2
- Simplifying:
AD=
⎷(11−168)2+(3√158)2=
⎷(−58)2+(3√158)2
=√2564+13564=√16064=√2.5
7. Evaluate Cosine Values:
- For cosB:
cosB=AB2+BC2−AC22⋅AB⋅BC=22+42−322⋅2⋅4=4+16−916=1116
- For cosC:
cosC=AC2+BC2−AB22⋅AC⋅BC=32+42−222⋅3⋅4=9+16−424=2124=78
Conclusion:
- We found:
- cosB=1116
- cosC=78
- AD2=2.5
- Therefore, the statements:
- cosB≠1116 is false.
- cosC≠78 is false.
- AD≠2.4 is true.
- AD2=2.5 is true.
Correct Statements:
- The correct statements are:
- Option 3: AD≠2.4 is true.
- Option 4: AD2=2.5 is true.
- Let A, B, and C be the vertices of the triangle.
- Place B at the origin (0,0) and C at (4,0) since BC=4.
- To find the coordinates of A, we can use the distances from B and C.
- The distance AB=2 gives us the equation:
√x2A+y2A=2(1)
- The distance AC=3 gives us the equation:
√(xA−4)2+y2A=3(2)
- Squaring both equations:
- From (1): x2A+y2A=4
- From (2): (xA−4)2+y2A=9
- Expanding (2):
x2A−8xA+16+y2A=9
- Substitute x2A+y2A=4 into the equation:
4−8xA+16=9
- Simplifying gives:
−8xA+20=9⟹−8xA=−11⟹xA=118
- Using x2A+y2A=4:
(118)2+y2A=4
12164+y2A=4⟹y2A=4−12164=256−12164=13564
- Thus, yA=±√13564=±√1358=±3√158.
- The coordinates of D (midpoint of BC):
D=(0+42,0+02)=(2,0)
- The length AD can be calculated using the distance formula:
AD=
⎷(118−2)2+(3√158)2
- Simplifying:
AD=
⎷(11−168)2+(3√158)2=
⎷(−58)2+(3√158)2
=√2564+13564=√16064=√2.5
- For cosB:
cosB=AB2+BC2−AC22⋅AB⋅BC=22+42−322⋅2⋅4=4+16−916=1116
- For cosC:
cosC=AC2+BC2−AB22⋅AC⋅BC=32+42−222⋅3⋅4=9+16−424=2124=78
- We found:
- cosB=1116
- cosC=78
- AD2=2.5
- Therefore, the statements:
- cosB≠1116 is false.
- cosC≠78 is false.
- AD≠2.4 is true.
- AD2=2.5 is true.
- The correct statements are:
- Option 3: AD≠2.4 is true.
- Option 4: AD2=2.5 is true.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
In a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionConstruct a triangle ABC with AB = 7 cm, BC = 3 cm, and CA = 5 cm.
View SolutionIn ΔABC, AB = 5cm , BC = 8 cm and CA = 7cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
View SolutionConstruct a triangle ABC in which AC=5cm, BC= 7 cm and AB= 6cm.
Mark D, the mid-point of AB
View SolutionThevertices of a triangle ABC are A(−7,8),B(5,2)andC(11,0). If D, E, F are the mid-points of the sides BC,CAandAB respectively, show that ΔABC=4ΔDEF.
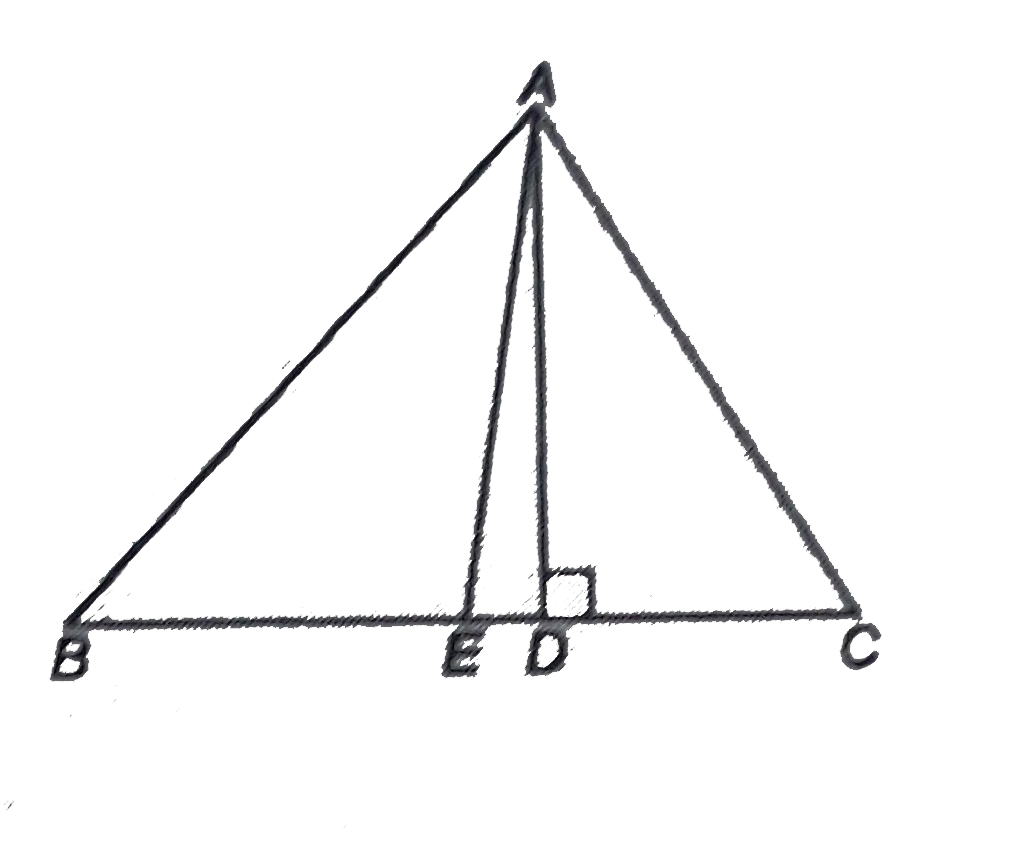
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View SolutionIf in a triangle ABC, the altitude AM be the bisector of ∠BAD, where D is the mid point of side BC, then prove that (b2−c2)=a22.
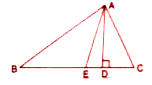
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIn a △ABC the sides BC=5,CA=4 and AB=3. If A(0,0) and the internal bisector of angle A meets BC in D (127,127) then incenter of △ABC is
View Solution
