In acute angled triangle ABC, AD is median and AE is altitude , prove that:
(i) AC2=AD2+BC×DE+14BC2
(ii) AB2=AD2−BC×DE+14BC2
(iii) AC2+AB2=2AD2+12BC2
To prove the given equations in the acute-angled triangle ABC where AD is the median and AE is the altitude, we will follow a systematic approach using the Pythagorean theorem and properties of triangles.
Step 1: Understanding the Triangle and Definitions
- Let triangle ABC be an acute-angled triangle with vertices A, B, and C.
- D is the midpoint of side BC (since AD is the median).
- E is the foot of the altitude from A to BC, making AE perpendicular to BC.
Step 2: Proving Equation (i)
We need to prove that:
AC2=AD2+BC⋅DE+14BC2
1. In triangle AEC, apply the Pythagorean theorem:
AC2=AE2+CE2
2. In triangle AED, again apply the Pythagorean theorem:
AD2=AE2+DE2⟹AE2=AD2−DE2
3. Since D is the midpoint of BC, we have:
CE=CD+DE=BC2+DE
4. Substitute CE into the equation for AC^2:
AC2=(AD2−DE2)+(BC2+DE)2
5. Expand (BC2+DE)2:
(BC2)2+DE2+2⋅BC2⋅DE=BC24+DE2+BC⋅DE
6. Substitute back into the equation for AC^2:
AC2=AD2−DE2+(BC24+DE2+BC⋅DE)
7. The DE^2 terms cancel out:
AC2=AD2+BC⋅DE+14BC2
Thus, the first equation is proved.
Step 3: Proving Equation (ii)
We need to prove that:
AB2=AD2−BC⋅DE+14BC2
1. In triangle ABE, apply the Pythagorean theorem:
AB2=AE2+BE2
2. Again, from triangle AED:
AE2=AD2−DE2
3. For BE, we have:
BE=BD−DE=BC2−DE
4. Substitute BE into the equation for AB^2:
AB2=(AD2−DE2)+(BC2−DE)2
5. Expand (BC2−DE)2:
(BC2)2+DE2−2⋅BC2⋅DE=BC24+DE2−BC⋅DE
6. Substitute back into the equation for AB^2:
AB2=AD2−DE2+(BC24+DE2−BC⋅DE)
7. The DE^2 terms cancel out:
AB2=AD2−BC⋅DE+14BC2
Thus, the second equation is proved.
Step 4: Proving Equation (iii)
We need to prove that:
AC2+AB2=2AD2+12BC2
1. From the results of (i) and (ii):
AC2+AB2=(AD2+BC⋅DE+14BC2)+(AD2−BC⋅DE+14BC2)
2. Combine the equations:
AC2+AB2=2AD2+(BC⋅DE−BC⋅DE)+14BC2+14BC2
3. The BC \cdot DE terms cancel out:
AC2+AB2=2AD2+12BC2
Thus, the third equation is proved.
- Let triangle ABC be an acute-angled triangle with vertices A, B, and C.
- D is the midpoint of side BC (since AD is the median).
- E is the foot of the altitude from A to BC, making AE perpendicular to BC.
We need to prove that:
AC2=AD2+BC⋅DE+14BC2
AC2=AE2+CE2
AD2=AE2+DE2⟹AE2=AD2−DE2
CE=CD+DE=BC2+DE
AC2=(AD2−DE2)+(BC2+DE)2
(BC2)2+DE2+2⋅BC2⋅DE=BC24+DE2+BC⋅DE
AC2=AD2−DE2+(BC24+DE2+BC⋅DE)
AC2=AD2+BC⋅DE+14BC2
We need to prove that:
AB2=AD2−BC⋅DE+14BC2
AB2=AE2+BE2
AE2=AD2−DE2
BE=BD−DE=BC2−DE
AB2=(AD2−DE2)+(BC2−DE)2
(BC2)2+DE2−2⋅BC2⋅DE=BC24+DE2−BC⋅DE
AB2=AD2−DE2+(BC24+DE2−BC⋅DE)
AB2=AD2−BC⋅DE+14BC2
We need to prove that:
AC2+AB2=2AD2+12BC2
AC2+AB2=(AD2+BC⋅DE+14BC2)+(AD2−BC⋅DE+14BC2)
AC2+AB2=2AD2+(BC⋅DE−BC⋅DE)+14BC2+14BC2
AC2+AB2=2AD2+12BC2
Similar Questions
In an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionIn an equilateral △ABC,AD is the altitude drawn from A on the side BC. Prove that 3AB2=4AD2
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionThe following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
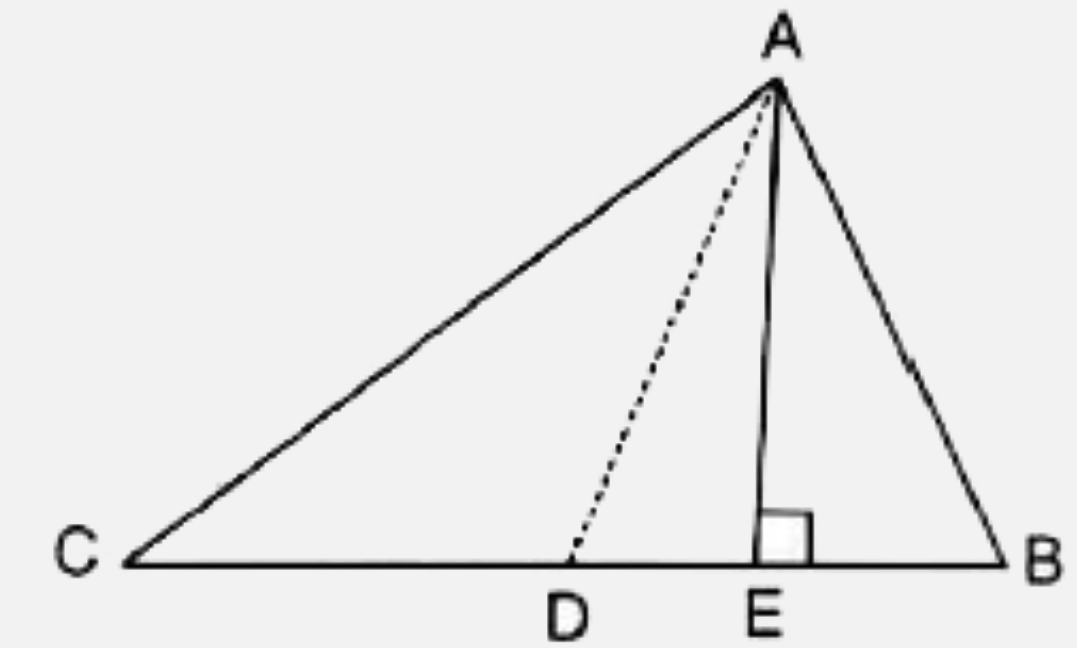
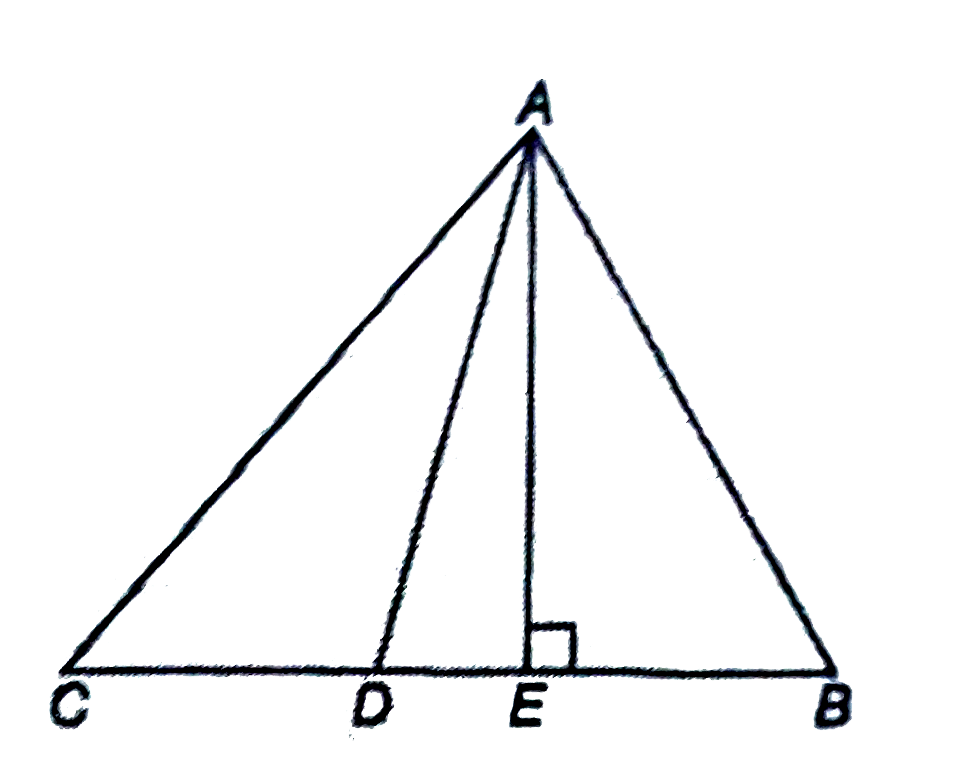
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
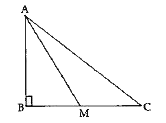
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View SolutionFind :
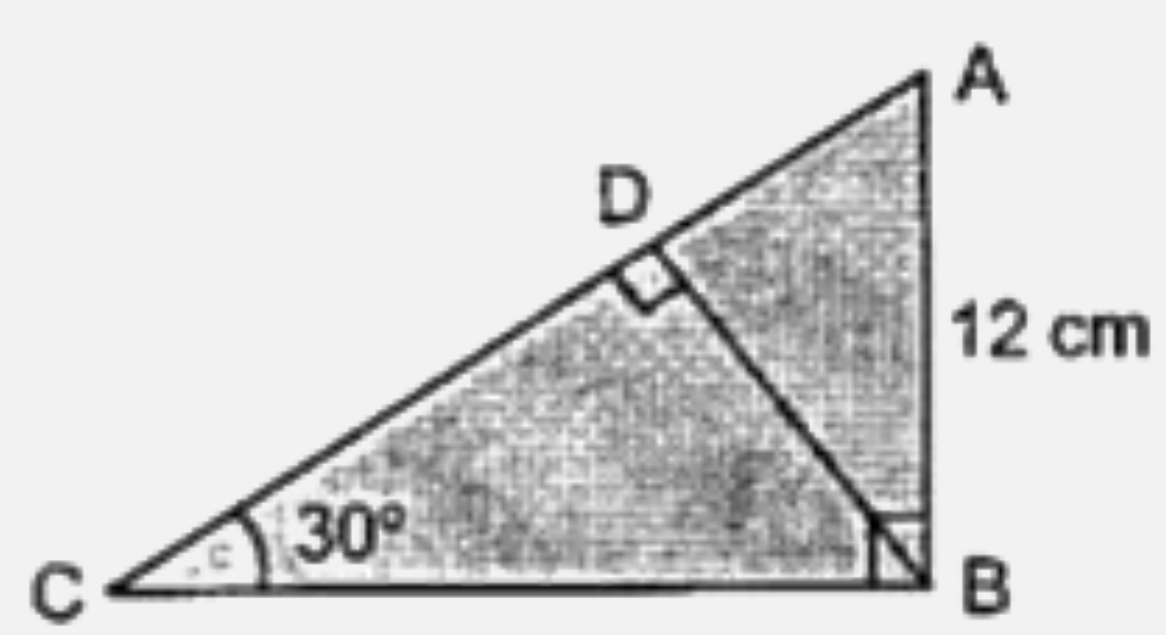
(i) BC
(ii) AD
(iii) AC
View Solution
