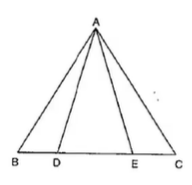
In an isosceles with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
Video Solution
Text Solution
GIVEN A D and E are point on BC such that BE=CD.
TO PROVE AD = AE.
PROOF
.
Now, in , we have
and
Hence,
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In a ΔABC, AB = AC and D is a point on AB, such that AD = DC = BC. Then, ∠BAC is
A40∘B45∘C30∘D36∘
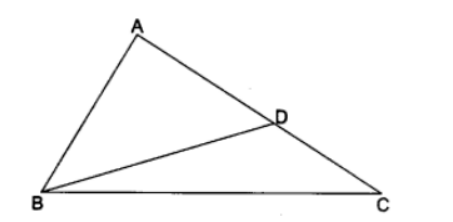
In ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
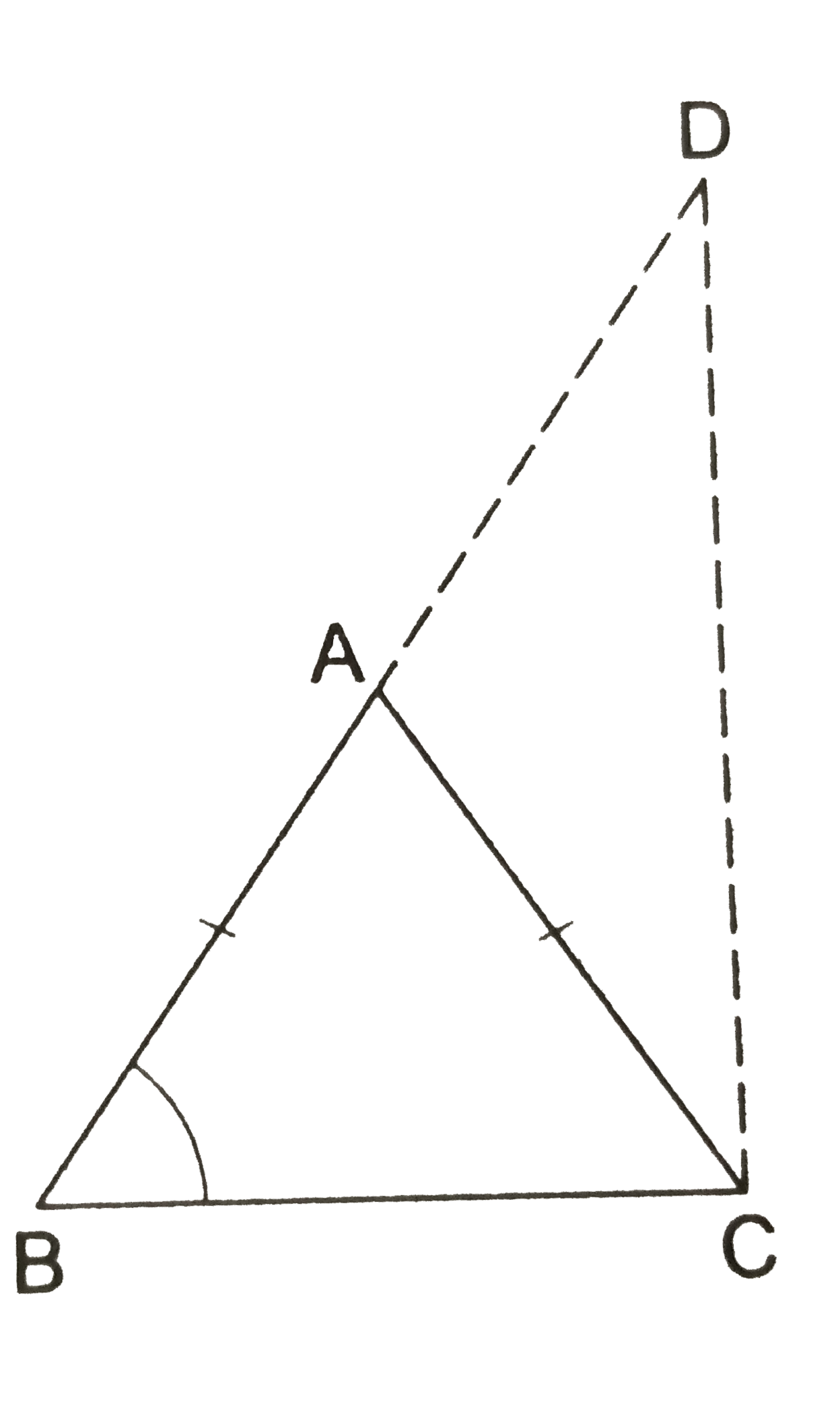
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
View SolutionIn a ΔABC,AB=AC,D is a point on BC such that ∠BAD=50∘ and a point E on side AC such that AE = AD find ∠CDE.
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View Solution