In ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
To prove that ar(ΔLOB)=ar(ΔMOC) given that LM∥BC in triangle ABC, we can follow these steps:
1. Identify the Triangles: We have triangle ABC and points L and M on sides AB and AC respectively, such that LM∥BC.
2. Use the Area Theorem: According to the theorem, triangles that are on the same base and between the same parallel lines have equal areas. Here, we will consider triangles LBC and MBC.
3. Establish Equality of Areas:
- Since LM∥BC, we can state that:
ar(ΔLBC)=ar(ΔMBC)
- This is because both triangles share the same base BC and are between the same parallel lines LM and BC.
4. Express Areas of Larger Triangles:
- We can express the area of triangle LBC as:
ar(ΔLBC)=ar(ΔLOB)+ar(ΔBOC)
- Similarly, for triangle MBC:
ar(ΔMBC)=ar(ΔMOC)+ar(ΔBOC)
5. Set the Two Area Expressions Equal:
- Since we established that ar(ΔLBC)=ar(ΔMBC), we can substitute the area expressions:
ar(ΔLOB)+ar(ΔBOC)=ar(ΔMOC)+ar(ΔBOC)
6. Cancel Common Areas:
- We can subtract ar(ΔBOC) from both sides:
ar(ΔLOB)=ar(ΔMOC)
7. Conclusion: Thus, we have proven that:
ar(ΔLOB)=ar(ΔMOC)
- Since LM∥BC, we can state that:
ar(ΔLBC)=ar(ΔMBC)
- This is because both triangles share the same base BC and are between the same parallel lines LM and BC.
- We can express the area of triangle LBC as:
ar(ΔLBC)=ar(ΔLOB)+ar(ΔBOC)
- Similarly, for triangle MBC:
ar(ΔMBC)=ar(ΔMOC)+ar(ΔBOC)
- Since we established that ar(ΔLBC)=ar(ΔMBC), we can substitute the area expressions:
ar(ΔLOB)+ar(ΔBOC)=ar(ΔMOC)+ar(ΔBOC)
- We can subtract ar(ΔBOC) from both sides:
ar(ΔLOB)=ar(ΔMOC)
ar(ΔLOB)=ar(ΔMOC)
Topper's Solved these Questions
Similar Questions
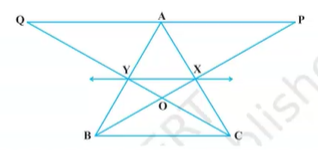
In figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
 View Solution
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
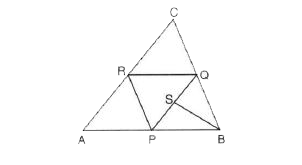
View SolutionThe following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : ar.(ΔABC)=8×ar.(ΔQSB)
 View Solution
View SolutionGiven a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCDView SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
 View Solution
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
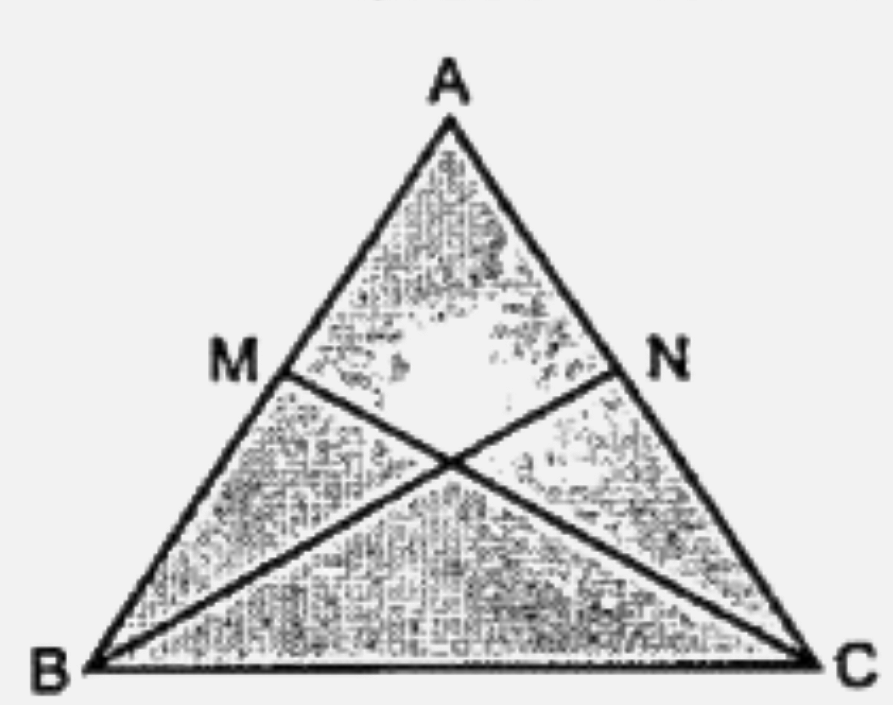
ΔBMC≅ΔCNBView SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that

ΔAMC≅ΔANBView SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.
 View Solution
View Solution
