In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that
Given, ABC and ABD are two triangle on the same base AB.
The line segment CD is bisected by AB at O. (.:OC=OD)
In ΔACD, we have
OC=OD (given)
∴AO is the median.
Since, the median divides a triangle in two triangles of equal areas.
∴ar(ΔAOC)=ar(ΔAOD)...(1)
Similarly, in ΔBCD, ar(ΔBOC)=ar(ΔBOD)...(2)
On adding (1) and (2), we get
ar(ΔAOC)+ar(ΔBOC)=ar(ΔAOD)+ar(ΔBOD)
⇒ar(ΔABC)=ar(ABD)
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In Figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar (△ABC)=ar ( △ABD)
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
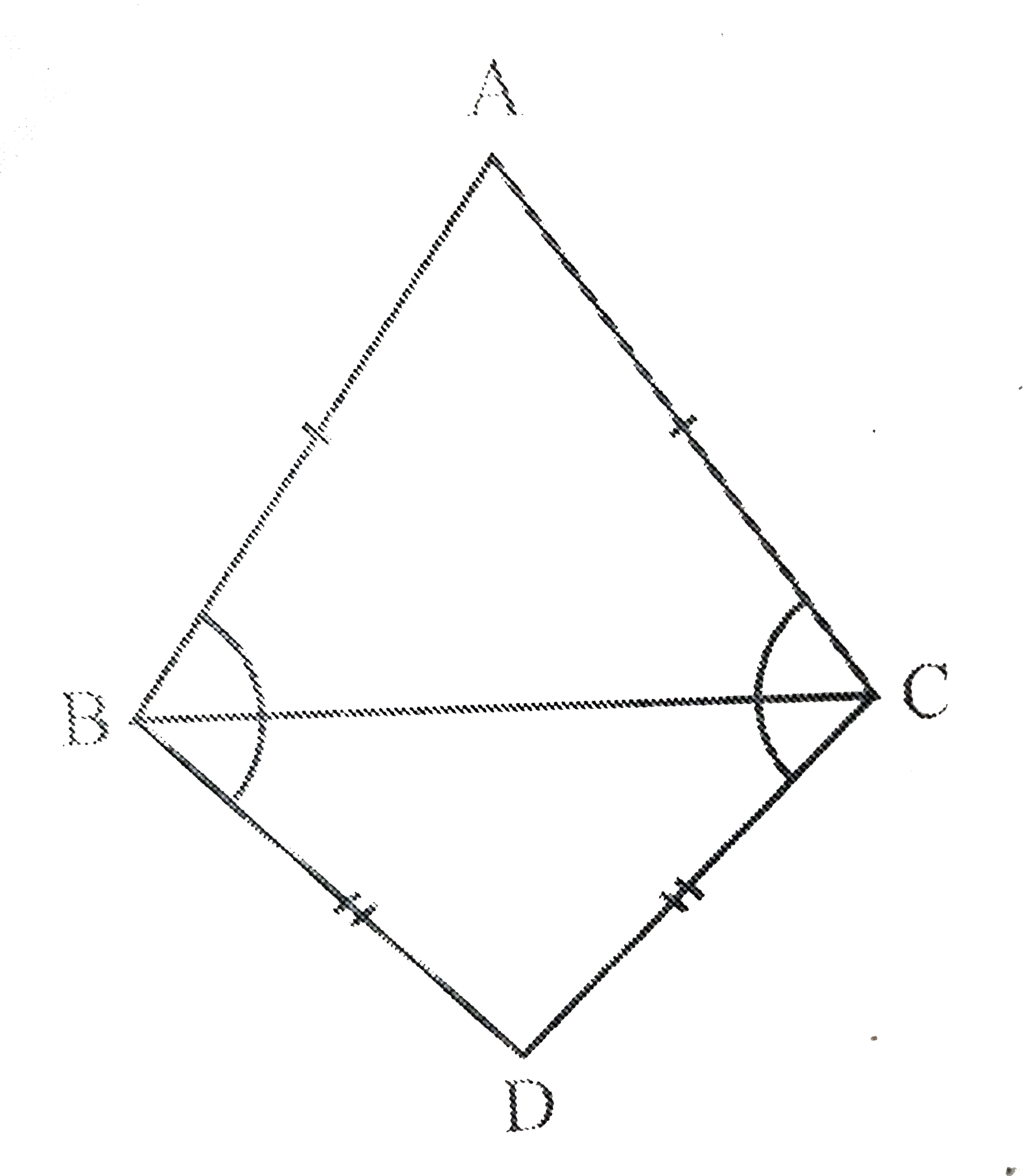
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionIn the given figure, AB∣∣CD. The line segments BC and AD intersect at O. Show that : z=x+y.

View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.
View SolutionIn Fig. 6.28, find the values of x and y and then show that AB || CD.

View SolutionAB is a line segment and M is its mid point. Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all thethree semi- circles. Show that AB=6×r
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
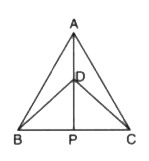
View SolutionThe given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that:
ΔABD=ΔACD
(ii) ΔABP=ΔACP
(iii) AP bisects ∠BDC
(iv) AP is perpendicular bisector of BC.
View Solution
