In fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
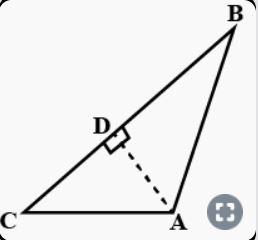
In △ADC, ∠ADC=90∘
∴(AC)2=(AD)2+(CD)2
(By Pythagoras theorem) .......... (1)
In △DBA,∠ADB=90∘
∴(AB)2=(AD)2+(BD)2
(By Pythagoras theorem) .......... (2)
Subtracting (1) from (2), we get
(AB)2−(AC)2=(AD)2+(BD)2−(AD)2−(CD)2
∴(AB)2−(AC)2=(BD)2−(CD)2
∴(AB)2+(CD)2=(BD)2+(AC)2
Topper's Solved these Questions
Similar Questions
In Fig. 5.10, if AC=BD, then prove that AB=CD.
 View Solution
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
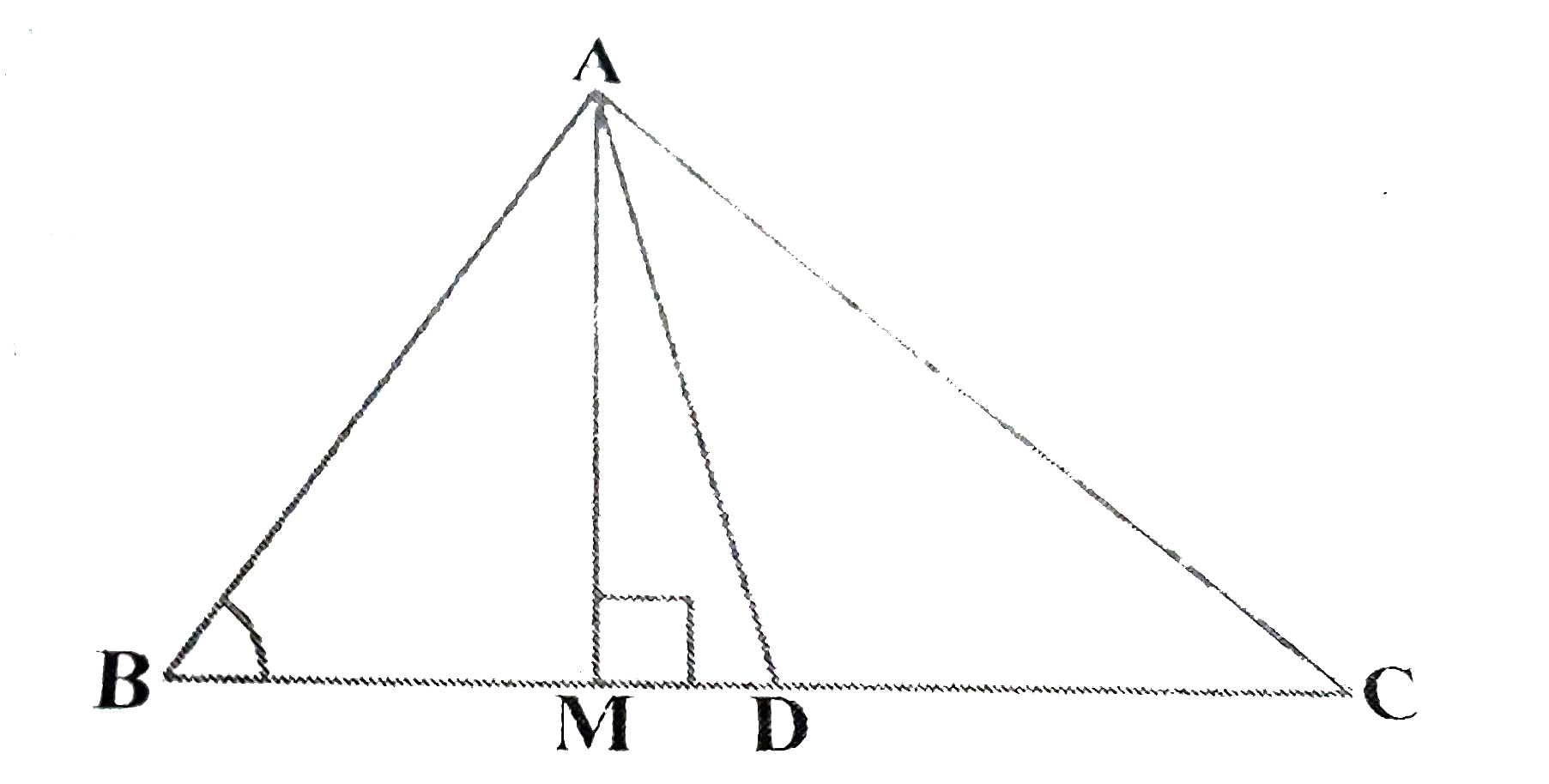
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
 View Solution
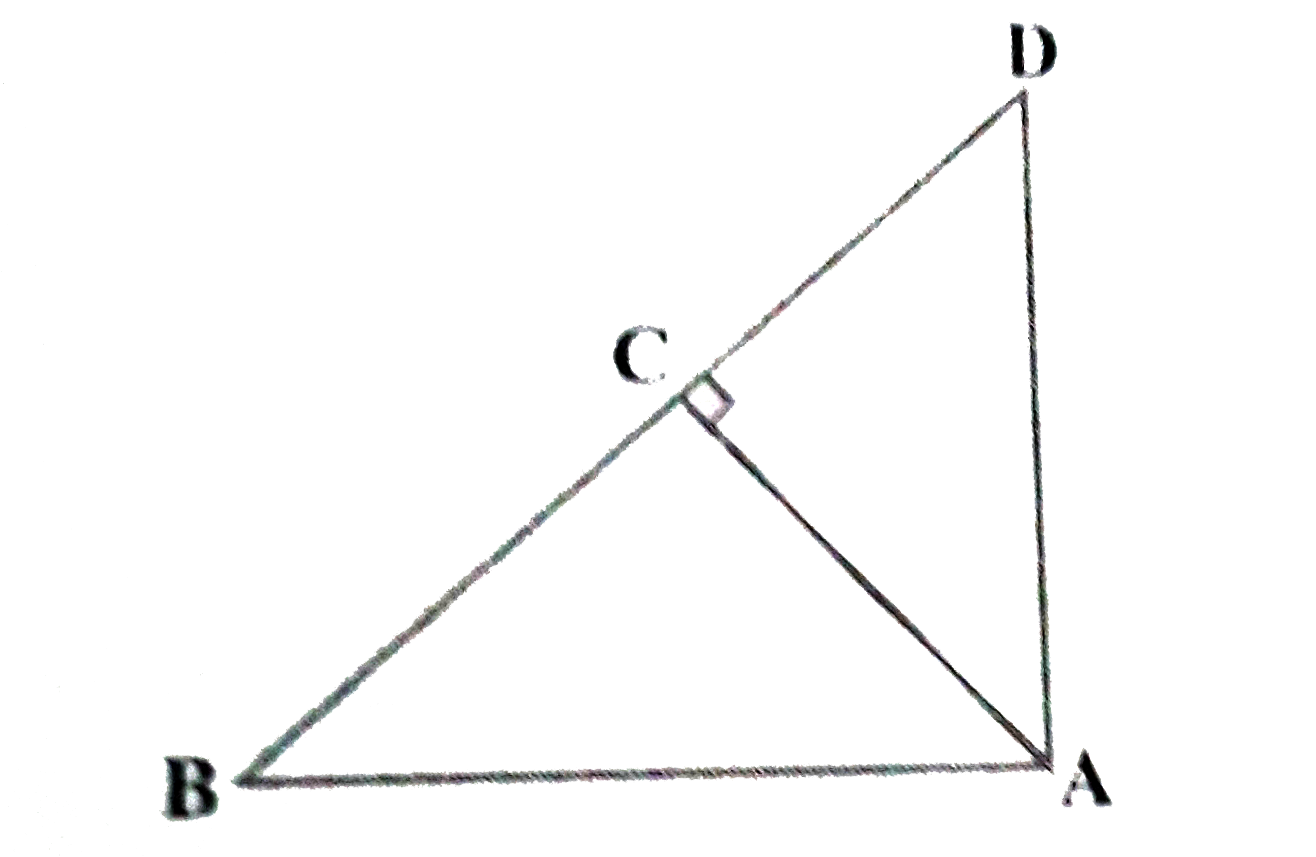
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
 View Solution
View SolutionIn Fig. 4.95, if ∠ADE=∠B show that ADE~ABC . If AD=3.8cm , AE=3.6cm , BE=2.1cm and BC=4.2cm , find DE . (FIGURE)
View Solution

