In figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.

Given-
AD is the angular bisector of a △ABC.
AD meets BC at D.
AD is the bisector of ∠BAC.
∴∠BAD=∠CAD.
Again , inΔACD,∠ADC is the external angle .
We know that the external angle of a triangle is greater than each internal opposite angle of the same triangle.
∴∠ADB=∠DAC+DCA.
=∠BAD+∠DCA(∵∠DAC=∠BAD)
i.e∠ADC>∠BAD.
∴BA>BD.
So option B is true.
∠ADC>∠BAD or ∠CAD
∴CD>CA
AD is the bisector of
∠BAC
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 6.316videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES14videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Exercise 6.210videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.28videos
SURFACE AREAS AND VOLUMES
Similar Questions
In a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960
 View Solution
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
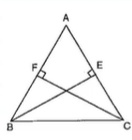
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
 View Solution
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionIn fig., D is a point on hypotenuse AC of ΔABC,DM⊥BCand DN⊥AB. Prove that
(i) DM2=DN⋅MC
(ii) DN2=DM⋅AN
 View Solution
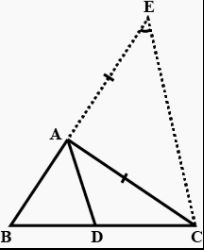
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.
 View Solution
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
 View Solution
View Solution

