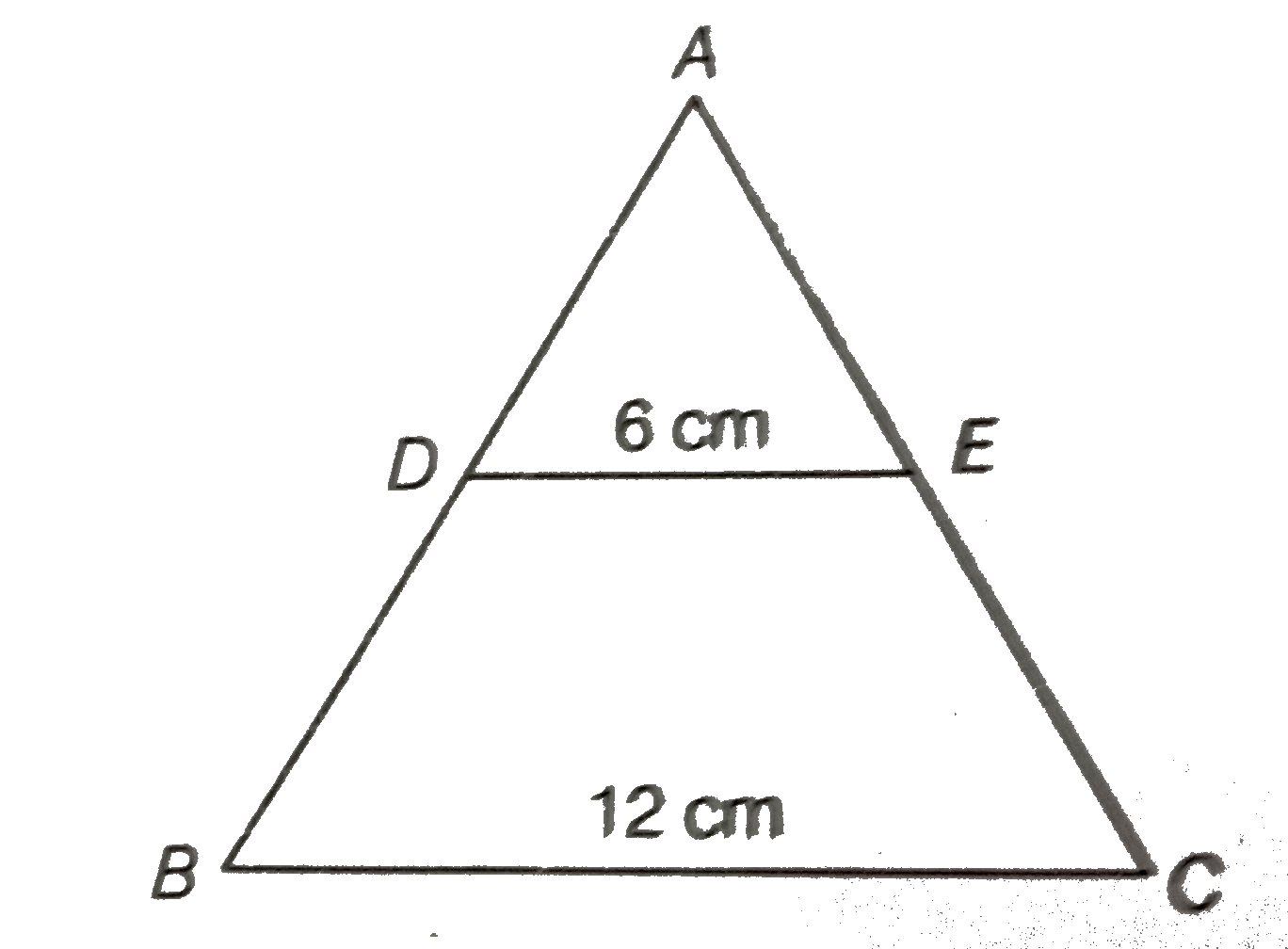
In figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
To solve the problem step by step, we will follow the reasoning provided in the video transcript and break it down into clear steps.
Step 1: Understand the Given Information
We are given that DE is parallel to BC and the ratio of the areas of triangle ADE and trapezium BDEC is 4:5. We also know that BD = 2 cm. We need to find the ratio of DE to BC and the length of AD.
Step 2: Use the Area Ratio
Let the area of triangle ADE be AADE and the area of trapezium BDEC be ABDEC. According to the problem:
AADEABDEC=45
Step 3: Relate Areas
The area of trapezium BDEC can be expressed as:
ABDEC=AABC−AADE
Thus, we can write:
AADEAABC−AADE=45
Step 4: Set Up the Equation
From the area ratio, we can express this as:
5⋅AADE=4⋅(AABC−AADE)
Expanding this gives:
5AADE=4AABC−4AADE
Combining like terms:
9AADE=4AABC
Thus, we can express the ratio of the areas:
AADEAABC=49
Step 5: Use Similar Triangles
Since DE || BC, triangles ADE and ABC are similar. The ratio of their areas is equal to the square of the ratio of their corresponding sides:
AADEAABC=(DEBC)2
Substituting the area ratio we found:
49=(DEBC)2
Step 6: Find the Ratio of DE to BC
Taking the square root of both sides:
DEBC=23
Step 7: Relate AD and AB
Using the same reasoning for the sides, we have:
ADAB=49
Thus:
AD=49⋅AB
Step 8: Express AB in Terms of AD and BD
Since AB=AD+BD, we can substitute:
AB=AD+2
Substituting this into the previous equation gives:
AD=49⋅(AD+2)
Step 9: Solve for AD
Multiplying through by 9 to eliminate the fraction:
9AD=4(AD+2)
Expanding:
9AD=4AD+8
Rearranging gives:
5AD=8
Thus:
AD=85=1.6 cm
Step 10: Final Calculation
Since we were given that BD = 2 cm, we can substitute back to find AD:
AD=4 cm
Final Answers
1. The ratio of DE to BC is 23.
2. The length of AD is 4 cm.
We are given that DE is parallel to BC and the ratio of the areas of triangle ADE and trapezium BDEC is 4:5. We also know that BD = 2 cm. We need to find the ratio of DE to BC and the length of AD.
Let the area of triangle ADE be AADE and the area of trapezium BDEC be ABDEC. According to the problem:
AADEABDEC=45
The area of trapezium BDEC can be expressed as:
ABDEC=AABC−AADE
Thus, we can write:
AADEAABC−AADE=45
From the area ratio, we can express this as:
5⋅AADE=4⋅(AABC−AADE)
Expanding this gives:
5AADE=4AABC−4AADE
Combining like terms:
9AADE=4AABC
Thus, we can express the ratio of the areas:
AADEAABC=49
Since DE || BC, triangles ADE and ABC are similar. The ratio of their areas is equal to the square of the ratio of their corresponding sides:
AADEAABC=(DEBC)2
Substituting the area ratio we found:
49=(DEBC)2
Taking the square root of both sides:
DEBC=23
Using the same reasoning for the sides, we have:
ADAB=49
Thus:
AD=49⋅AB
Since AB=AD+BD, we can substitute:
AB=AD+2
Substituting this into the previous equation gives:
AD=49⋅(AD+2)
Multiplying through by 9 to eliminate the fraction:
9AD=4(AD+2)
Expanding:
9AD=4AD+8
Rearranging gives:
5AD=8
Thus:
AD=85=1.6 cm
Since we were given that BD = 2 cm, we can substitute back to find AD:
AD=4 cm
1. The ratio of DE to BC is 23.
2. The length of AD is 4 cm.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a24videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
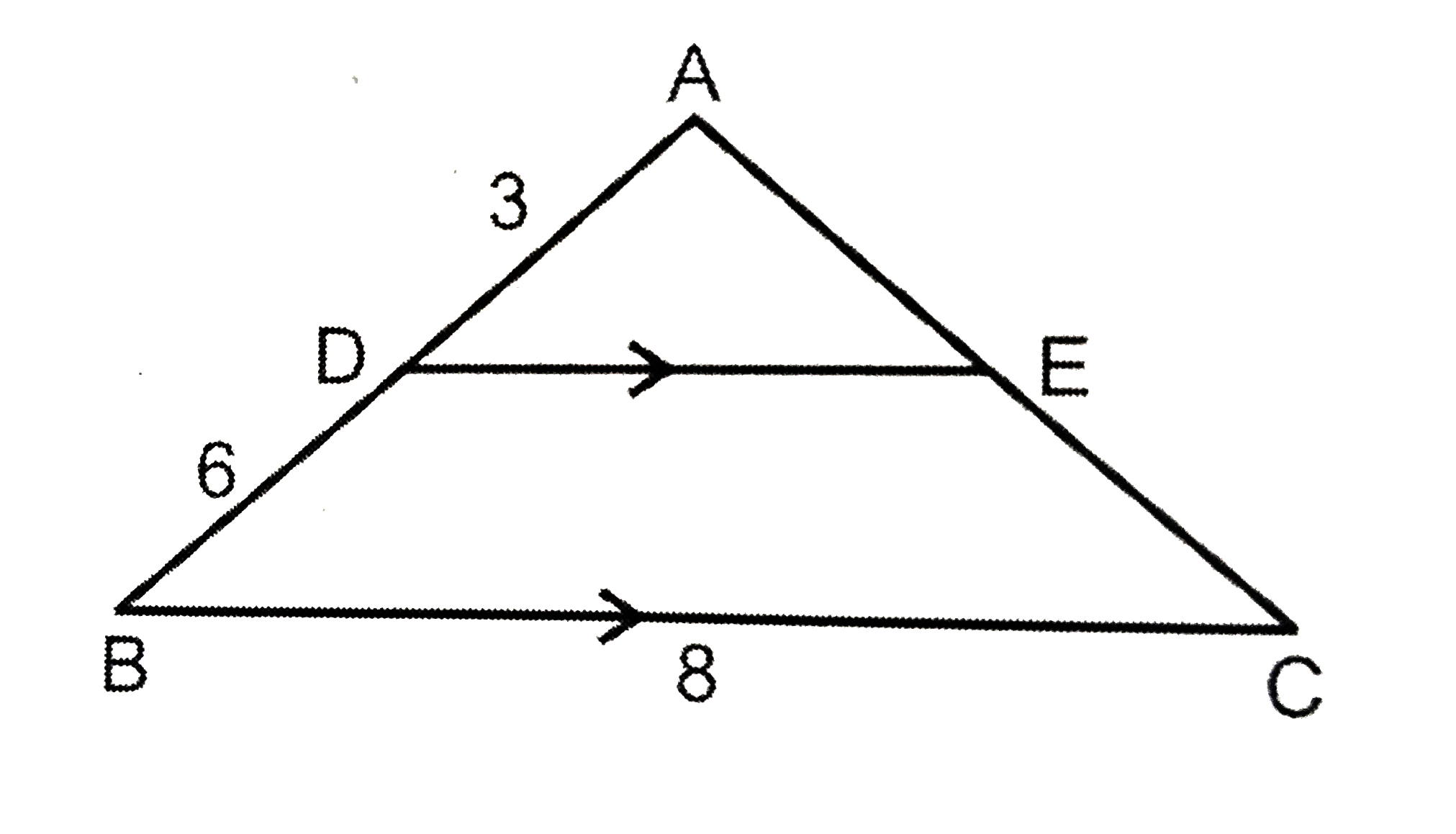
In the ΔABC,DE||BC, AD=3, BD=6, and BC=8. What is the ratio of the areas of triangle ADE and trapezium BDEC?A1:3B1:4C1:8D1:9
In the given figure, AX:XB=3:5

Find :
the ratio between the areas of trapezium XBCY and triangle ABC.View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
ADAB and then DEBCView SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

Area of ΔDEFArea ofΔBFCView SolutionIn Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
View SolutionIn the adjoining figure, DE//BC and D divides AB in the ratio 2 : 3. Find DE, if BC = 7.5 cm.
 View Solution
View SolutionFind BC, if the area of the triangle ABC is 36cm2 and the height AD is 3cm (Fing 11.21)
View SolutionIn the given figure, BC is parallel to DE. Area of triangle ABC=25cm2, Area of trapezium BCED=24cm2andDE=14cm. Calculate the length of BC.
Also, find the area of triangle BCD.
 View Solution
View Solution