Question

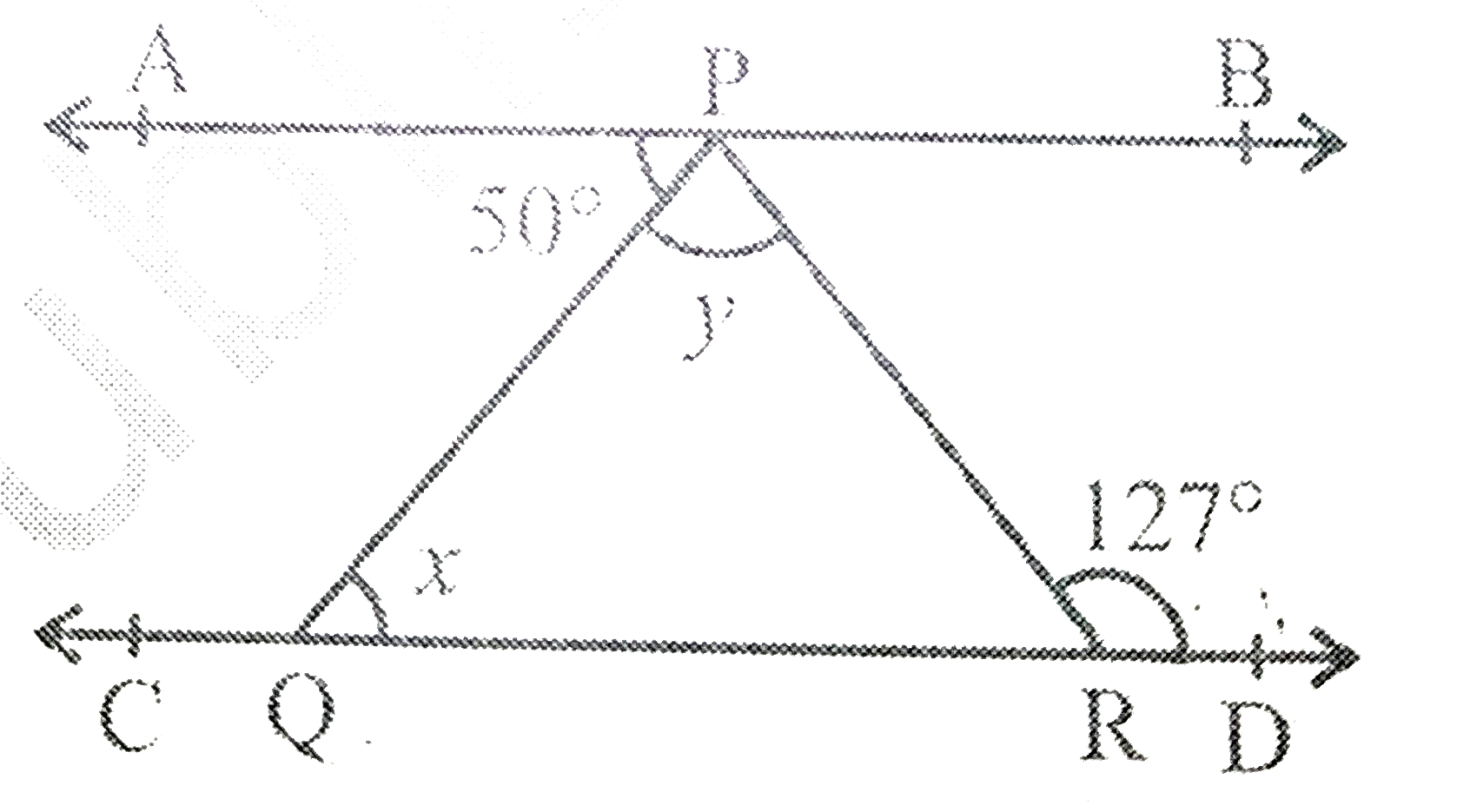
In Figure, if $AB\mid \mid CD,\angle APQ={50}^{0}AND\angle PRD={127}^0,$
find $xandy$

Explanation

To solve the problem, we need to find the values of angles $$x$$ and $$y$$ given the conditions in the figure. Here’s the step-by-step solution:

Step 1: Identify the Given Information
- We have two parallel lines \( AB \) and \( CD \).
- The angle \( \angle APQ = 50^\circ \).
- The angle \( \angle PRD = 127^\circ \).

Step 2: Use the Properties of Parallel Lines
Since \( AB \) is parallel to \( CD \) and \( PQ \) is a transversal, we can use the property of alternate interior angles.

Step 3: Find Angle \( x \)
- The angle \( \angle APQ \) corresponds to \( \angle PQR \) (which is \( x \)).
- According to the alternate interior angles theorem, since \( AB \parallel CD \), we have:
\( \angle APQ = \angle PQR \)
- Therefore, we can conclude:
\( x = 50^\circ \)

Step 4: Find Angle \( y \)
- Now, we look at the angles formed by the transversal \( PR \) with the parallel lines \( AB \) and \( CD \).
- The angle \( \angle APR \) is equal to \( \angle PRD \) because they are corresponding angles.
- Given that \( \angle PRD = 127^\circ \), we have:
\( \angle APR = y \)
- Therefore, we can conclude:
\( y = 127^\circ \)

Final Answer
- The values are:
\( x = 50^\circ, \quad y = 127^\circ \)