In Figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC+∠ACD=900 .
To prove that ∠BAC + ∠ACD = 90°, we will follow these steps:
Step 1: Identify the elements of the circle
Let O be the center of the circle, and let BCD be the tangent to the circle at point C.
Step 2: Establish that OC is perpendicular to BCD
Since BCD is a tangent to the circle at point C, we know that the radius OC is perpendicular to the tangent line BCD at point C. Therefore, we can write:
∠OCD=90∘
Step 3: Use the properties of the triangle OAC
In triangle OAC, we have:
- OA = OC (both are radii of the circle).
Since OA = OC, triangle OAC is an isosceles triangle. Therefore, the angles opposite to equal sides are equal:
∠OAC=∠OCA
Step 4: Relate angles BAC and ACD to angles OAC and ACD
Now, we can express angles BAC and ACD in terms of angles OAC and OCA:
- ∠BAC = ∠OAC
- ∠ACD = ∠OCA
Step 5: Add the angles
Now, we can add these two angles:
∠BAC+∠ACD=∠OAC+∠OCA
Step 6: Use the triangle angle sum property
In triangle OAC, the sum of angles is:
∠OAC+∠OCA+∠OCD=180∘
Since we already established that:
∠OCD=90∘
We can substitute this into the equation:
∠OAC+∠OCA+90∘=180∘
Step 7: Solve for ∠OAC + ∠OCA
Rearranging gives us:
∠OAC+∠OCA=180∘−90∘=90∘
Conclusion
Thus, we have shown that:
∠BAC+∠ACD=90∘
This completes the proof.
---
Let O be the center of the circle, and let BCD be the tangent to the circle at point C.
Since BCD is a tangent to the circle at point C, we know that the radius OC is perpendicular to the tangent line BCD at point C. Therefore, we can write:
∠OCD=90∘
In triangle OAC, we have:
- OA = OC (both are radii of the circle).
∠OAC=∠OCA
Now, we can express angles BAC and ACD in terms of angles OAC and OCA:
- ∠BAC = ∠OAC
- ∠ACD = ∠OCA
Now, we can add these two angles:
∠BAC+∠ACD=∠OAC+∠OCA
In triangle OAC, the sum of angles is:
∠OAC+∠OCA+∠OCD=180∘
Since we already established that:
∠OCD=90∘
We can substitute this into the equation:
∠OAC+∠OCA+90∘=180∘
Rearranging gives us:
∠OAC+∠OCA=180∘−90∘=90∘
Thus, we have shown that:
∠BAC+∠ACD=90∘
This completes the proof.
Topper's Solved these Questions
Similar Questions
In Figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC+∠ACD=900 .
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
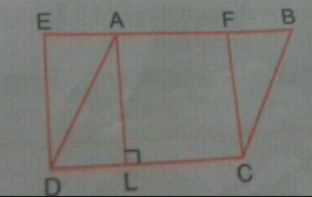
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL⊥DC. Prove that : ar(ABCD)=ar(EFCD) ar(ABCD)=DC×AL

View SolutionBisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
View SolutionIn Figure, O is the centre of the circle and ∠BDC=420. The measure of ∠ACB is 420 (b) 480 (c) 580 (d) 520
View SolutionIn Figure, O is the centre of the circle such that ∠AOC =1300, then ∠ABC= 1300 (b) 1150 (c) 650 (d) 1650
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
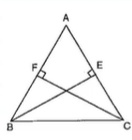
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View Solution
